3259. Из точек A
и B
, лежащих вне окружности, проведены к окружности касательные AM
, AN
и BK
, BL
(M
, N
, K
, L
— точки касания). Докажите, что точки A
, B
и середины хорд MN
и KL
лежат на одной окружности.
Указание. Пусть O
центр окружности, P
и Q
— середины хорд MN
и KL
. Докажите, что OP\cdot OA=OQ\cdot OB
.
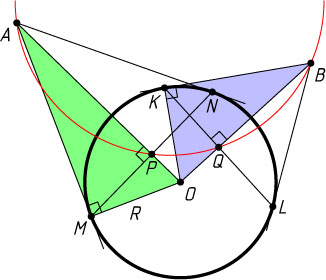
Решение. Пусть O
— центр окружности радиуса R
, P
и Q
— середины хорд MN
и KL
. Тогда MP
и KQ
— высоты прямоугольных треугольников AOM
и BOK
, проведённые из вершин прямых углов. Поэтому
OP\cdot OA=OM^{2}=R^{2},~OQ\cdot OB=OK^{2}=R^{2},
значит, OP\cdot OA=OQ\cdot OB
. Следовательно, точки A
, B
, P
и Q
лежат на одной окружности (см. задачу 0114).
Источник: Пржевальский Е. Собрание геометрических теорем и задач. — М.: Типография Г. Лисснера и Д. Собко, 1909. — № 175, с. 90
