3287. Дан треугольник ABC
со сторонами AB=3
, AC=\sqrt{73}
медианой AM=4
.
а) Докажите, что медиана AM
перпендикулярна стороне AB
.
б) Найдите высоту треугольника ABC
, проведённую из вершины A
.
Ответ. 2,4.
Указание. На продолжении медианы AM
за точку M
отложите отрезок MD=AM
.
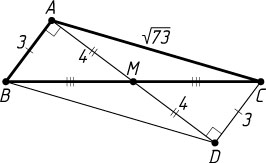
Решение. а) На продолжении медианы AM
за точку M
отложим отрезок MD=AM=4
(рис. 1). Тогда ABDC
— параллелограмм. Поэтому CD=AB=3
и CD\parallel AB
. Треугольник ACD
прямоугольный с прямым углом при вершине D
, так как AC^{2}=73=64+9=AD^{2}+CD^{2}
. Следовательно, \angle BAM=\angle ADC=90^{\circ}
.
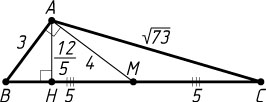
б) Пусть AH
— высота треугольника ABC
(рис. 2). Из прямоугольного треугольника AMB
находим, что BM=5
. Следовательно,
AH=\frac{AB\cdot AM}{BM}=\frac{3\cdot4}{5}=\frac{12}{5}.
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 2.19, с. 21
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 2.19.1, с. 20

