3290. Четырёхугольник ABCD
вписан в окружность с центром O
. Диагонали четырёхугольника перпендикулярны, пересекаются в точке P
, отличной от O
, и не проходят через точку O
. Точки M
и N
— середины диагоналей AC
и BD
соответственно.
а) Докажите, что прямая OP
проходит через середину отрезка MN
.
б) Найдите площадь четырёхугольника OMPN
, если известно, что AC=BD
, а MN=10
.
Ответ. 50.
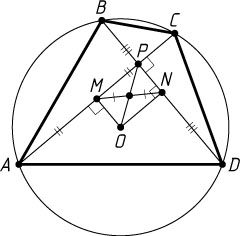
Решение. а) Диаметр, проходящий через середину хорды, не являющейся диаметром, перпендикулярен этой хорде, поэтому четырёхугольник OMPN
— прямоугольник (рис. 1). Диагонали прямоугольника точкой пересечения делятся пополам, следовательно, прямая OP
проходит через середину MN
.
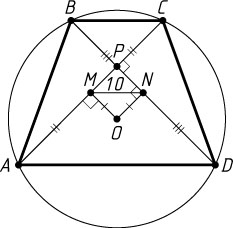
б) Равные хорды равноудалены от центра окружности, поэтому прямоугольник OMPN
— квадрат (рис. 2). Его диагонали равны 10. Следовательно, его площадь равна 50.
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 3.25, с. 30
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 3.25.1, с. 28

