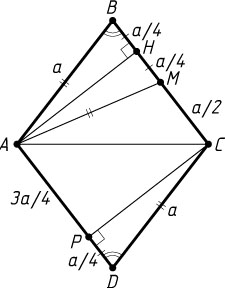
3291. Отрезок, соединяющий вершину A
ромба ABCD
с серединой стороны BC
, равен стороне ромба.
а) Докажите, что высота ромба, проведённая из вершины C
, делит сторону AD
на отрезки, один из которых втрое больше другого.
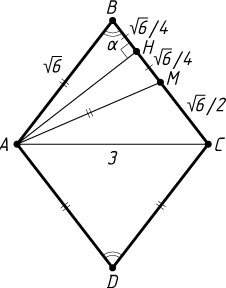
б) Найдите диагональ AC
ромба, если известно, что сторона ромба равна \sqrt{6}
.
Ответ. 3.
Решение. а) Пусть M
— середина стороны BC
ромба (рис. 1), AH
— высота ромба, опущенная на сторону BC
. Поскольку треугольник ABM
равнобедренный (AM=AB
), точка H
— середина отрезка BM
. Обозначим BC=a
. Тогда
AM=AB=a,~BH=\frac{1}{2}BM=\frac{1}{2}\cdot\frac{1}{2}BC=\frac{a}{4}.
Значит, CH=3BH
.
Пусть CP
— высота ромба, опущенная на сторону AD
. Прямоугольные треугольники CPD
и AHB
равны, поэтому DP=BH
. Значит, \frac{DP}{AP}=\frac{BH}{CH}=\frac{1}{3}
. Следовательно, AP=3DP
.
б) Обозначим \angle ABC=\alpha
. Из прямоугольного треугольника AHB
(рис. 2) находим, что \cos\alpha=\frac{BH}{AB}=\frac{1}{4}
. Следовательно,
AC=\sqrt{AB^{2}+BC^{2}-2AB\cdot BC\cos\alpha}=\sqrt{6+6-2\sqrt{6}\cdot\sqrt{6}\cdot\frac{1}{4}}=\sqrt{9}=3.
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 3.27, с. 30
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 3.28.1, с. 29

