3292. Окружность, построенная на стороне AD
параллелограмма ABCD
как на диаметре, проходит через точку пересечения диагоналей параллелограмма.
а) Докажите, что ABCD
— ромб.
б) Эта окружность пересекает сторону AB
в точке M
, причём AM:MB=2:1
. Найдите диагональ AC
, если известно AD=\sqrt{6}
.
Ответ. 2\sqrt{5}
.
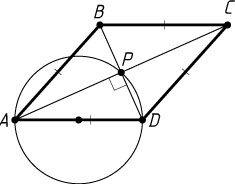
Решение. а) Пусть P
— точка пересечения диагоналей параллелограмма ABCD
(рис. 1). Точка P
лежит на окружности с диаметром AD
, значит, \angle APD=90^{\circ}
, т. е. AC\perp BD
. Параллелограмм, диагонали которого перпендикулярны, есть ромб.
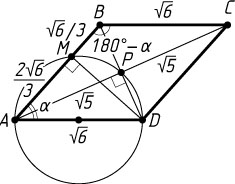
б) Точка M
также лежит на окружности с диаметром AD
, значит, \angle AMD=90^{\circ}
(рис. 2). При этом AM=\frac{2}{3}AB=\frac{2}{3}AD
. Обозначим \angle BAD=\alpha
. Из прямоугольного треугольника AMD
находим, что \cos\alpha=\frac{AM}{AD}=\frac{2}{3}
. Тогда
\cos\angle ABC=\cos(180^{\circ}-\alpha)=-\cos\alpha=-\frac{2}{3}.
Следовательно,
AC=\sqrt{AB^{2}+BC^{2}-2AB\cdot BC\cos\angle ABC}=\sqrt{6+6+2\cdot6\cdot\frac{2}{3}}=\sqrt{20}=2\sqrt{5}.
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 3.28, с. 30
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 3.29.1, с. 30

