3294. Точки E
, F
, G
и H
— середины сторон соответственно AB
, BC
, CD
и AD
выпуклого четырёхугольника ABCD
. Точки M
и N
— середины диагоналей AC
и BD
соответственно.
а) Докажите, что отрезки EG
, FH
и MN
пересекаются в одной точке.
б) Найдите отношение площадей четырёхугольников EMGN
и FMHN
, если AC=BD
, AC\perp BD
, а прямые MN
и FH
пересекаются под углом \alpha
.
Ответ. \ctg\alpha
.
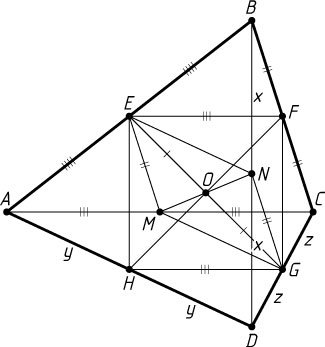
Решение. а) Отрезки EF
и GH
— средние линии треугольников ABC
и ADC
(рис. 1), поэтому EF=\frac{1}{2}AC=GH
и EF\parallel AC\parallel GH
. Значит, четырёхугольник EFGH
— параллелограмм. Его диагональ FH
проходит через середину O
диагонали EG
.
Отрезки EM
и GN
— средние линии треугольников ABC
и DBC
, поэтому EM=\frac{1}{2}BC=GN
и EM\parallel BC\parallel GN
. Значит, четырёхугольник EMGN
— также параллелограмм. Его диагональ MN
проходит через середину диагонали EG
, т. е. через точку O
.
Следовательно, отрезки EG
, FH
и MN
пересекаются в точке O
.
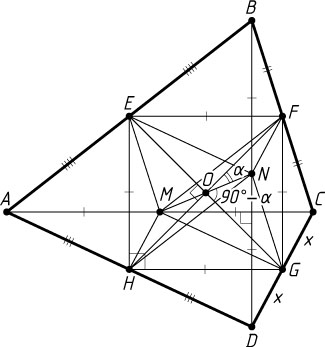
б) Поскольку диагонали AC
и BD
четырёхугольника ABCD
равны, равны и стороны параллелограмма EFGH
(рис. 2), значит, это ромб, а так как AC\perp BD
, то это квадрат, и EG=FH
. Его диагонали EG
и FH
перпендикулярны, значит, угол между диагоналями EG
и MN
параллелограмма EMGN
равен 90^{\circ}-\alpha
. Поэтому
S_{EMGN}=\frac{1}{2}EG\cdot MN\sin(90^{\circ}-\alpha)=\frac{1}{2}EG\cdot MN\cos\alpha.
Четырёхугольник FMHN
— также параллелограмм. Угол между его диагоналями FH
и MN
равен \alpha
, поэтому
S_{FMHN}=\frac{1}{2}FH\cdot MN\sin\alpha.
Следовательно,
\frac{S_{EMGN}}{S_{FMHN}}=\frac{\frac{1}{2}EG\cdot MN\cos\alpha}{\frac{1}{2}FH\cdot MN\sin\alpha}=\frac{\cos\alpha}{\sin\alpha}=\ctg\alpha.
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 3.31, с. 31

