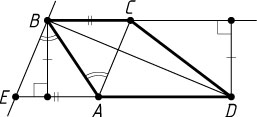
3296. Через вершину B
трапеции ABCD
с основаниями AD
и BC
проведена прямая, параллельная диагонали AC
. Пусть эта прямая пересекается с продолжением основания AD
в точке E
.
а) Докажите, что треугольник DBE
равновелик трапеции ABCD
.
б) Найдите площадь трапеции, диагонали которой равны 10 и 24, а средняя линия равна 13.
Ответ. 120.
Решение. а) Противоположные стороны AE
и BC
четырёхугольника ACBE
попарно параллельны, значит, это параллелограмм (рис. 1). Поэтому AE=BC
. Треугольник BAE
равновелик DBC
, так как у них равны высоты, опущенные из вершин B
и D
на равные стороны AE
и BC
. Треугольник ABD
— общая часть трапеции ABCD
и треугольника DBE
, следовательно, S_{ABCD}=S_{\triangle DBE}
.
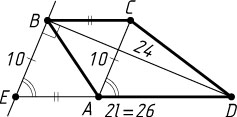
б) Пусть AC=10
, BD=24
, а средняя линия трапеции ABCD
равна l
(рис. 2). Тогда
l=\frac{1}{2}(BC+AD)=\frac{1}{2}(AE+AD)=\frac{1}{2}DE.
Отсюда находим, что DE=2l=26
. Треугольник DBE
прямоугольный, так как DE^{2}=676=100+576=BE^{2}+BD^{2}
, поэтому
S_{ABCD}=S_{\triangle BDE}=\frac{1}{2}BE\cdot BD=\frac{1}{2}BE\cdot BD=\frac{1}{2}\cdot10\cdot24=120.
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 4.40, с. 40
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 4.40.1, с. 39

