3297. Боковая сторона CD
трапеции ABCD
равна основанию AD
.
а) Докажите, что CA
— биссектриса угла BCD
.
б) Прямая, проходящая через вершину C
перпендикулярно CD
, пересекает боковую сторону AB
в точке M
. Найдите отношение BM:AM
, если известно, что AD=CD=2BC
и \angle ADC=60^{\circ}
.
Ответ. 1:2
.
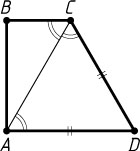
Решение. а) Треугольник ADC
равнобедренный (рис. 1), поэтому \angle ACD=\angle CAD=\angle ACB
. Следовательно, CA
— биссектриса угла BCD
.
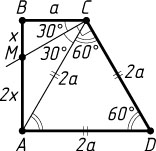
б) Обозначим BC=a
(рис. 2). Тогда AD=CD=2a
. Треугольник ADC
равносторонний, поэтому AC=2a
. CM
— биссектриса треугольника ABC
, так как
\angle BCM=\angle BCD-\angle MCD=120^{\circ}-90^{\circ}=30^{\circ}=\frac{1}{2}\angle ACB.
По свойству биссектрисы треугольника
\frac{BM}{AM}=\frac{BC}{AC}=\frac{a}{2a}=\frac{1}{2}.
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 4.41, с. 40
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 4.41.1, с. 39

