3298. Прямая, параллельная основаниям BC
и AD
трапеции ABCD
, пересекает боковые стороны AB
и CD
в точках M
и N
, а диагонали AC
и BD
— в точках K
и L
соответственно, причём точка K
лежит между M
и L
.
а) Докажите, что MK=NL
.
б) Найдите MN
, если известно, что BC=a
, AD=b
и MK:KL:LN=1:2:1
.
Ответ. \frac{4ab}{3a+b}
.
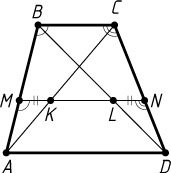
Решение. а) Треугольник AMK
подобен треугольнику ABC
по двум углам, причём коэффициент подобия равен \frac{AM}{AB}
(рис. 1). Треугольник DNL
подобен треугольнику DCB
с коэффициентом \frac{DN}{DC}
, а так как MN\parallel BC
, то \frac{DN}{DC}=\frac{AM}{AB}
. Значит,
MK=BC\cdot\frac{AM}{AB}=BC\cdot\frac{DN}{DC}=NL.
б) Пусть диагонали трапеции пересекаются в точке O
. Заметим, что точка K
не может лежать между O
и C
, так как в этом случае MK\gt KL
, что не соответствует условию задачи (MK:KL=1:2
).
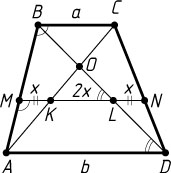
Следовательно, точка K
лежит между A
и O
(рис. 2). Обозначим MK=NL=x
. Тогда KL=2x
, ML=3x
.
Из подобия треугольников AMK
и ABC
следует, что \frac{x}{a}=\frac{MK}{BC}=\frac{AM}{AB}
. Из подобия треугольников MBL
и ABD
следует, что \frac{3x}{b}=\frac{ML}{AD}=\frac{BM}{AB}
. Сложив эти равенства, получим, что
\frac{x}{a}+\frac{3x}{b}=\frac{AM}{AB}+\frac{BM}{AB}=\frac{AM+BM}{AB}=\frac{AB}{AB}=1.
Из уравнения \frac{x}{a}+\frac{3x}{b}=1
находим, что x=\frac{ab}{3a+b}
. Следовательно, MN=4x=\frac{4ab}{3a+b}
.
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 4.42, с. 40
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 4.42.1, с. 39

