3299. В равнобедренную трапецию ABCD
с основаниями AD
и BC
вписана окружность, CH
— высота трапеции.
а) Докажите, что центр окружности, вписанной в трапецию, лежит на отрезке BH
.
б) Найдите диагональ AC
, если известно, что средняя линия трапеции равна 2\sqrt{7}
, а \angle AOD=120^{\circ}
, где O
— центр окружности, вписанной в трапецию, а AD
— большее основание.
Ответ. 7.
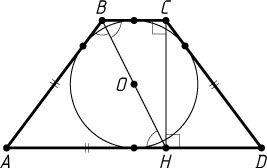
Решение. а) Поскольку трапеция равнобедренная, AH=\frac{1}{2}(AD+BC)
(рис. 1), а так как суммы противоположных сторон описанного четырёхугольника равны, то AD+BC=AB+CD=2AB=2CD
. Значит,
AB=\frac{1}{2}(AD+BC)=AH.
Треугольник ABH
равнобедренный, поэтому углы при его основании BH
равны. Тогда \angle CBH=\angle AHB=\angle ABH
, значит, BH
— биссектриса угла ABC
. Центр окружности, вписанной в угол, лежит на его биссектрисе, следовательно, центр O
окружности, вписанной в трапецию ABCD
, лежит на OH
.
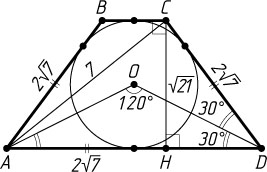
б) Точка O
лежит на биссектрисе угла ADC
(рис. 2), поэтому
\angle ADC=2\angle ADO=2(60^{\circ}-30^{\circ})=60^{\circ}.
Средняя линия трапеции равна полусумме оснований, поэтому AH=AB=CD=\frac{1}{2}(AD+BC)=2\sqrt{7}
. Из прямоугольного треугольника CDH
находим, что
CH=CD\sin60^{\circ}=2\sqrt{7}\cdot\frac{\sqrt{3}}{2}=\sqrt{21}.
Следовательно,
AC=\sqrt{AH^{2}+CH^{2}}=\sqrt{28+21}=7.
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 4.43, с. 40
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 4.43.1, с. 40

