3300. В треугольнике ABC
проведена медиана BM
. Известно, что \frac{\sin\angle ABM}{\sin\angle CBM}=\frac{1}{2}
. Найдите отношение \frac{BC}{AB}
.
Ответ. \frac{1}{2}
.
Указание. Достройте треугольник до параллелограмма и примените теорему синусов.
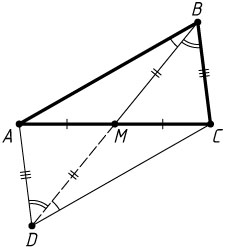
Решение. На продолжении медианы BM
за точку M
отложим отрезок MD
, равный BM
. Диагонали AC
и BD
четырёхугольника ABCD
делятся точкой пересечения M
пополам, значит, ABCD
— параллелограмм. Поэтому AD=BC
и \angle ADB=\angle CBM
. По теореме синусов из треугольника ABD
находим, что
\frac{AD}{AB}=\frac{\sin\angle ABD}{\sin\angle ADB}=\frac{\sin\angle ABM}{\sin\angle CBM}=\frac{1}{2}.
Следовательно, \frac{BC}{AB}=\frac{AD}{AB}=\frac{1}{2}
.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 2, с. 5
