3301. Стороны треугольника равны 3 и 6, а угол между ними равен 60^{\circ}
. Найдите биссектрису треугольника, проведённую из вершины этого угла.
Ответ. 2\sqrt{3}
.
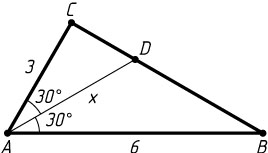
Решение. Пусть AD
— биссектриса треугольника ABC
, в котором AB=6
, AC=3
, \angle BAC=60^{\circ}
.
Первый способ. Обозначим AD=x
. Тогда
S_{\triangle ABC}=\frac{1}{2}AB\cdot AC\sin60^{\circ}=\frac{1}{2}\cdot6\cdot3\cdot\frac{\sqrt{3}}{2}=\frac{9\sqrt{3}}{2}.
С другой стороны,
S_{\triangle ABC}=S_{\triangle ABD}+S_{\triangle ACD}=\frac{1}{2}AB\cdot AD\sin30^{\circ}+\frac{1}{2}AC\cdot AD\sin30^{\circ}=\frac{1}{2}\cdot6\cdot x\cdot\frac{1}{2}+\frac{1}{2}\cdot3\cdot x\cdot\frac{1}{2}=\frac{9}{4}x.
Из уравнения \frac{9}{4}x=\frac{9\sqrt{3}}{2}
находим, что x=2\sqrt{3}
.
Второй способ. Заметим, что треугольник ABC
прямоугольный. Тогда треугольник ACD
также прямоугольный, причём \angle CAD=30^{\circ}
. Следовательно,
AD=\frac{AC}{\cos\angle CAD}=\frac{3}{\cos30^{\circ}}=2\sqrt{3}.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 5, с. 5
