3302. Точки M
и N
— середины сторон соответственно BC
и CD
параллелограмма ABCD
. Отрезки AM
и BN
пересекаются в точке O
. Найдите отношение \frac{MO}{OA}
.
Ответ. \frac{1}{4}
.
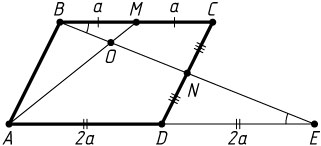
Решение. Пусть продолжения отрезков BN
и AD
пересекаются в точке E
. Обозначим BM=CM=a
. Тогда AD=BC=2a
.
Треугольник DNE
равен треугольнику CNB
по стороне и прилежащим к ней углам, поэтому DE=BC=2a
. Значит, AE=AD+DE=2a+2a=4a
.
Треугольник BOM
подобен треугольнику EOA
, следовательно,
\frac{MO}{OA}=\frac{BM}{AE}=\frac{a}{4a}=\frac{1}{4}.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 6, с. 5
