3303. Из точки M
, лежащей вне окружности с центром O
и радиусом R
, проведены касательные MA
и MB
(A
и B
— точки касания). Прямые OA
и MB
пересекаются в точке C
. Найдите OC
, если известно, что отрезок OM
делится окружностью пополам.
Ответ. 2R
.
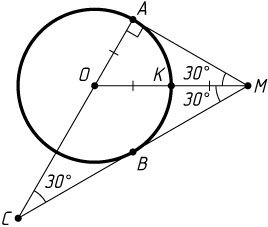
Решение. Пусть K
— точка пересечения окружности с отрезком OM
. Тогда OM=2OK=2R
. В прямоугольном треугольнике OAM
катет OA
вдвое меньше гипотенузы OM
, значит, \angle AMO=30^{\circ}
, а так как MO
— биссектриса угла AMC
, то \angle AMC=60^{\circ}
. Из прямоугольного треугольника MAC
находим, что \angle ACM=30^{\circ}
, значит, треугольник MOC
— равнобедренный. Следовательно, OC=OM=2R
.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 8, с. 5
