3305. На катетах прямоугольного треугольника как на диаметрах построены окружности. Найдите их общую хорду, если катеты равны 3 и 4.
Ответ. \frac{12}{5}
.
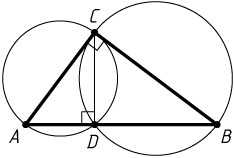
Решение. Пусть CD
— общая хорда окружностей, построенных на катетах AC=3
и BC=4
прямоугольного треугольника ABC
как на диаметрах. Тогда \angle ADC=\angle BDC=90^{\circ}
как вписанные углы, опирающиеся на диаметр. Значит, точка D
лежит на гипотенузе AB
, а CD
— высота прямоугольного треугольника ABC
, проведённая из вершины прямого угла.
По теореме Пифагора AB=\sqrt{9+16}=5
, а так как S_{\triangle ABC}=\frac{1}{2}AC\cdot BC
и S_{\triangle ABC}=\frac{1}{2}AB\cdot CD
, то \frac{1}{2}AC\cdot BC=\frac{1}{2}AB\cdot CD
, откуда находим, что
CD=\frac{AC\cdot BC}{AB}=\frac{3\cdot4}{5}=\frac{12}{5}.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 10, с. 5
