3306. Найдите радиусы вписанной и описанной окружностей треугольника со сторонами 13, 13, 24 и расстояние между центрами этих окружностей.
Ответ. 16{,}9
; 2{,}4
; 14{,}3
.
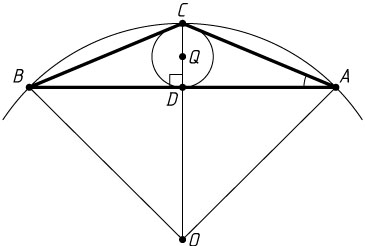
Решение. Пусть CD
— высота равнобедренного треугольника ABC
со сторонами AC=BC=13
и AB=24
, O
— центр его описанной окружности радиуса R
, Q
— центр вписанной окружности радиуса r
. Из прямоугольного треугольника ACD
находим, что
CD=\sqrt{AC^{2}-AD^{2}}=\sqrt{13^{2}-12^{2}}=5,
\sin\angle CAD=\frac{CD}{AC}=\frac{5}{13}.
По теореме синусов
R=\frac{BC}{2\sin\angle BAC}=\frac{13}{2\cdot\frac{5}{13}}=16{,}9.
Радиус окружности, вписанной в треугольник, равен площади треугольника, делённой на его полупериметр, поэтому
r=\frac{S_{\triangle ABC}}{AC+AD}=\frac{AD\cdot CD}{AC+AD}=\frac{12\cdot5}{13+12}=2{,}4.
Заметим, что угол CAD
меньше 45^{\circ}
, так как его тангенс меньше 1 (\tg\angle CAD=\frac{CD}{AC}=\frac{5}{12}\lt1
), значит, угол ACB
— тупой, поэтому точки O
и Q
лежат по разные стороны от прямой AB
. Следовательно,
OQ=OC-CQ=OC-(CD-QD)=R-(CD-r)=16{,}9-(5-2{,}4)=14{,}3.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 11, с. 5
