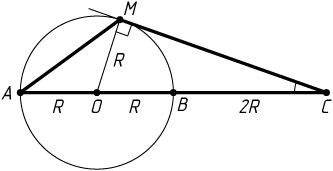
3307. На продолжении диаметра AB
окружности отложен отрезок BC
, равный диаметру. Прямая, проходящая через точку C
, касается окружности в точке M
. Найдите площадь треугольника ACM
, если радиус окружности равен R
.
Ответ. \frac{4}{3}R^{2}\sqrt{2}
.
Решение. Пусть O
— центр окружности. Тогда OM\perp CM
. В прямоугольном треугольнике OMC
известно, что OM=R
и OC=OB+BC=R+2R=3R
. Тогда
CM=\sqrt{OC^{2}-OM^{2}}=\sqrt{9R^{2}-R^{2}}=2R\sqrt{2},
\sin\angle OCM=\frac{OM}{OC}=\frac{R}{3R}=\frac{1}{3}.
Следовательно,
S_{\triangle ACM}=\frac{1}{2}AC\cdot CM\sin\angle ACM=\frac{1}{2}\cdot2R\sqrt{2}\cdot4R\cdot\frac{1}{3}=\frac{4}{3}R^{2}\sqrt{2}.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 12, с. 6
