3308. Окружность S_{1}
проходит через центр окружности S_{2}
и пересекает её в точках A
и B
. Хорда AC
окружности S_{1}
касается окружности S_{2}
в точке A
и делит первую окружность на дуги, градусные меры которых относятся как 5:7
. Найдите градусные меры дуг, на которые окружность S_{2}
делится окружностью S_{1}
.
Ответ. 150^{\circ}
и 210^{\circ}
.
Решение. Пусть O_{1}
и O_{2}
— центры окружностей S_{1}
и S_{2}
соответственно. Тогда
\angle AO_{1}C=360^{\circ}\cdot\frac{5}{5+7}=150^{\circ}.
Поскольку \angle O_{2}AC=90^{\circ}
(радиус, проведённый в точку касания, перпендикулярен касательной), отрезок O_{2}C
— диаметр окружности S_{1}
, поэтому
\angle AO_{2}C=\frac{1}{2}\angle AO_{1}C=75^{\circ}.
Тогда градусная мера дуги окружности S_{2}
, заключённой между сторонами угла AO_{2}C
, равна 75^{\circ}
, а градусная мера дуги AB
окружности S_{2}
, содержащейся внутри окружности S_{1}
, равна 150^{\circ}
. Следовательно, дополнительная к ней дуга окружности S_{2}
равна 360^{\circ}-150^{\circ}=210^{\circ}
.
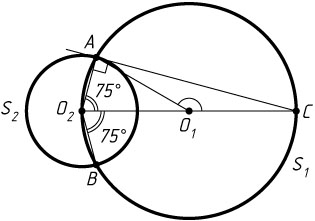
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 13, с. 6
