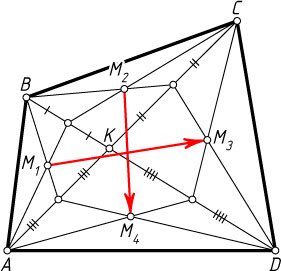
3309. Диагонали AC
и BD
четырёхугольника ABCD
пересекаются в точке K
. Пусть M_{1}
, M_{2}
, M_{3}
, M_{4}
— точки пересечения медиан треугольников ABK
, BCK
, CDK
, ADK
соответственно. Разложите векторы \overrightarrow{M_{1}M_{3}}
и \overrightarrow{M_{2}M_{4}}
по векторам \overrightarrow{AC}
и \overrightarrow{BD}
.
Ответ. \overrightarrow{M_{1}M_{3}}=\frac{1}{3}(\overrightarrow{AC}+\overrightarrow{BD})
; \overrightarrow{M_{2}M_{4}}=\frac{1}{3}(\overrightarrow{BD}-\overrightarrow{AC})
.
Решение. Поскольку M_{1}
и M_{3}
— точки пересечения медиан треугольников ABK
и BDK
,
\overrightarrow{M_{1}M_{3}}=\frac{1}{3}(\overrightarrow{AC}+\overrightarrow{BD}+\overrightarrow{KK})=\frac{1}{3}(\overrightarrow{AC}+\overrightarrow{BD}+\overrightarrow{0})=\frac{1}{3}(\overrightarrow{AC}+\overrightarrow{BD}).
Аналогично
\overrightarrow{M_{2}M_{4}}=\frac{1}{3}(\overrightarrow{BD}+\overrightarrow{CA}+\overrightarrow{KK})=\frac{1}{3}(\overrightarrow{BD}-\overrightarrow{AC}+\overrightarrow{0})=\frac{1}{3}(\overrightarrow{BD}-\overrightarrow{AC}).