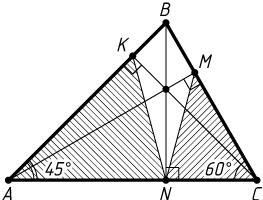
3310. Углы при вершинах A
и C
треугольника ABC
равны 45^{\circ}
и 60^{\circ}
соответственно; AM
, BN
и CK
— высоты треугольника. Найдите отношение \frac{MN}{KN}
.
Ответ. \frac{\sqrt{3}}{2}
.
Решение. Из прямоугольных треугольников BNC
и AMC
находим, что
CN=BC\cos60^{\circ}=\frac{1}{2}BC,~CM=AC\cos60^{\circ}=\frac{1}{2}AC,
поэтому \frac{CN}{CM}=\frac{\frac{1}{2}BC}{\frac{1}{2}AC}=\frac{BC}{AC}
. Значит, треугольник CMN
подобен треугольнику CAB
по двум сторонам и углу между ними (угол C
— общий), причём коэффициент подобия равен \frac{CM}{AC}=\frac{1}{2}
. Следовательно, MN=\frac{1}{2}AB
.
Аналогично получим, что треугольник AKN
подобен треугольнику ACB
, причём коэффициент подобия равен \frac{\sqrt{2}}{2}
. Значит, KN=\frac{\sqrt{2}}{2}BC
.
По теореме синусов
\frac{AB}{BC}=\frac{\sin60^{\circ}}{\sin45^{\circ}}=\frac{\frac{\sqrt{3}}{2}}{\frac{\sqrt{2}}{2}}=\frac{\sqrt{3}}{\sqrt{2}}.
Следовательно,
\frac{MN}{KN}=\frac{\frac{1}{2}AB}{\frac{\sqrt{2}}{2}BC}=\frac{\sqrt{2}}{2}\cdot\frac{AB}{BC}=\frac{\sqrt{2}}{2}\cdot\frac{\sqrt{3}}{\sqrt{2}}=\frac{\sqrt{3}}{2}.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 15, с. 6
