3311. Около треугольника со сторонами 6, 8 и 10 описана окружность S
. Найдите радиус окружности, касающейся меньшей стороны треугольника в её середине и окружности S
.
Ответ. \frac{1}{2}
или \frac{9}{2}
.
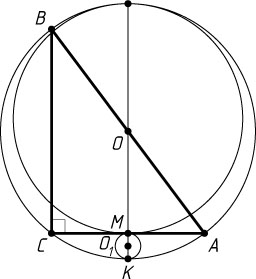
Решение. Пусть O
— центр окружности, описанной около треугольника ABC
со сторонами AC=6
, BC=8
и AB=10
. Треугольник ABC
— прямоугольный (AC^{2}+BC^{2}=36+64=100=AB^{2}
), Поэтому O
— середина его гипотенузы AB
, а радиус окружности равен 5.
Пусть O_{1}
— центр окружности радиуса r
, касающейся катета BC
в его середине M
и касающейся в точке K
внутренним образом описанной окружности треугольника ABC
, причём точки O
и O_{1}
расположены по разные стороны от прямой AC
. Линия центров касающихся окружностей проходит через точку их касания, поэтому OK=OM+MK=OM+2O_{1}K
, а так как OM
— средняя линия треугольника ABC
, OM=\frac{1}{2}BC=4
, OK=5
— радиус описанной окружности треугольника ABC
и MK
— диаметр искомой окружности, то 5=4+2r
. Следовательно, r=\frac{1}{2}
.
Если же точки O
и O_{1}
расположены по одну сторону от прямой AC
, то аналогично находим, что r=\frac{9}{2}
.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — Диагностическая работа 1, задача 1
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 1, с. 164
