3312. Дан треугольник со сторонами AB=BC=17
, AC=30
. Найдите общую хорду окружностей с диаметрами AB
и AC
.
Ответ. \frac{240}{17}
.
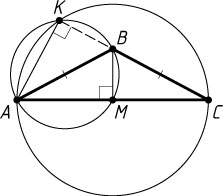
Решение. Пусть окружность с диаметром AB
вторично пересекает прямую AC
в точке M
. Тогда BM
— высота, а значит, медиана треугольника ABC
. По теореме Пифагора BM=\sqrt{17^{2}-15^{2}}=8\lt15
, поэтому в прямоугольном треугольнике ABM
угол при вершине B
больше 45^{\circ}
. Следовательно, \angle ABC\gt90^{\circ}
.
Пусть окружность с диаметром AC
вторично пересекает прямую BC
в точке K
. Тогда AK
— высота тупоугольного треугольника ABC
, поэтому точка K
лежит на продолжении боковой стороны BC
за точку B
.
Из точки K
отрезок AB
виден под прямым углом, значит, эта точка лежит на окружности с диаметром AB
. Таким образом, K
— вторая точка пересечения окружностей, о которых говорится в условии задачи, а AK
— общая хорда этих окружностей.
Из равенства BC\cdot AK=AC\cdot BM
находим, что
AK=\frac{AC\cdot BM}{BC}=\frac{30\cdot8}{17}=\frac{240}{17}.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — Диагностическая работа 1, задача 2
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 2, с. 164
