3313. Окружность касается сторон AB
и AD
прямоугольника ABCD
и пересекает сторону DC
в единственной точке F
, а сторону BC
— в единственной точке E
. Найдите площадь трапеции AFCB
, если AB=32
, AD=40
и BE=1
.
Ответ. 1180.
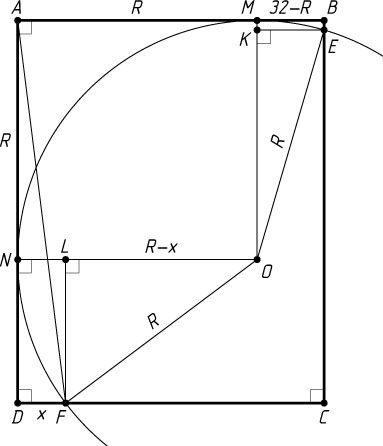
Решение. Пусть окружность радиуса R
с центром O
касается сторон AB
и AD
прямоугольника ABCD
в точках M
и N
соответственно. В прямоугольной трапеции OMBE
известно, что
OM=OE=R,~BM=AB-AM=AB-ON=32-R,~BE=1.
Из точки E
опустим перпендикуляр EK
на OM
. Тогда
OK=OM-MK=OM-BE=R-1,~KE=BM=32-R.
Рассмотрим прямоугольный треугольник OKE
. По теореме Пифагора OE^{2}=OK^{2}+KE^{2}
, или
R^{2}=(R-1)^{2}+(32-R)^{2},~R^{2}-66R+1025=0.
Условию задачи удовлетворяет R=25
.
В прямоугольной трапеции DFON
известно, что
OF=ON=R=25,~DN=AD-AN=40-R=15.
Обозначим DF=x
. Из точки F
опустим перпендикуляр FL
на ON
. Тогда
OL=ON-LN=ON-DF=R-x=25-x,~FL=DN=15.
Рассмотрим прямоугольный треугольник OLF
. По теореме Пифагора OF^{2}=OL^{2}+FL^{2}
, или
25^{2}=(25-x)^{2}+15^{2},~x^{2}-50x+225=0.
Условию задачи удовлетворяет x=5
. Тогда CF=CD-x=32-5=27
.
Следовательно,
S_{AFCB}=\frac{CF+AB}{2}\cdot BC=\frac{27+32}{2}\cdot40=1180.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — Диагностическая работа 1, задача 4
Источник: Вступительный экзамен на факультет почвоведения МГУ. — 1979, вариант 4, № 4
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Наука, 1983. — с. 78
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 4, с. 164
