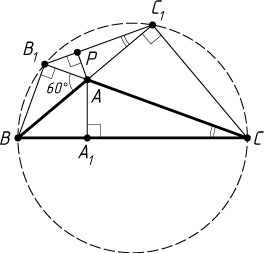
3314. В треугольнике ABC
проведены высоты AA_{1}
, BB_{1}
и CC_{1}
. Известно, что \angle BAC=120^{\circ}
и AA_{1}=6
. Найдите высоту AP
треугольника AB_{1}C_{1}
.
Ответ. 3.
Решение. Из точек B_{1}
и C_{1}
отрезок BC
виден под прямым углом, значит, эти точки лежат на окружности с диаметром BC
. Вписанные в эту окружность углы BC_{1}B_{1}
и BCB_{1}
опираются на одну и ту же дугу, поэтому они равны.
Треугольник B_{1}AC_{1}
подобен треугольнику BAC
по двум углам, причём коэффициент подобия равен
\frac{AB_{1}}{AB}=\cos\angle BAB_{1}=\cos60^{\circ}=\frac{1}{2}.
При этом подобии высота AP
треугольника B_{1}AC_{1}
соответствует высоте AA_{1}
треугольника BAC
, следовательно, AP=\frac{1}{2}AA_{1}=\frac{1}{2}\cdot6=3
.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — Диагностическая работа 1, задача 5
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 5, с. 164
