3315. Центр окружности, вписанной в четырёхугольник, лежит на его диагонали, равной 5. Известно, что периметр четырёхугольника равен 14, а площадь равна 12. Найдите вторую диагональ и стороны четырёхугольника.
Ответ. \frac{24}{5}
, 3, 4, 3, 4.
Решение. Пусть AC=5
— диагональ данного четырёхугольника ABCD
, O
— центр вписанной в четырёхугольник окружности. Центр окружности, вписанной в угол, лежит на биссектрисе этого угла, поэтому треугольники ABC
и ADC
равны по стороне и двум прилежащим к ней углам.
Обозначим AB=AD=x
, BC=CD=y
, \angle ABC=\alpha
. Тогда
x+y=7,~\frac{1}{2}xy\sin\alpha=6,~xy=\frac{12}{\sin\alpha},~x^{2}+y^{2}-2xy\cos\alpha=25,
x^{2}+y^{2}-2xy\cos\alpha=(x+y)^{2}-2xy-2xy\cos\alpha=49-2xy(1+\cos\alpha)=25,~xy=\frac{12}{1+\cos\alpha}.
Из равенства \frac{12}{1+\cos\alpha}=\frac{12}{\sin\alpha}
следует, что 1+\cos\alpha=\sin\alpha
. После возведения обеих частей этого уравнения в квадрат и очевидных упрощений получим уравнение \cos\alpha(1+\cos\alpha)=0
, а так как 0^{\circ}\lt\alpha\lt180^{\circ}
, то \alpha=90^{\circ}
.
Таким образом
\syst{x+y=7\\xy=12\\}
Из этой системы находим, что x=3
, y=4
или x=4
, y=3
.
Точки A
и C
равноудалены от концов отрезка BD
, значит, AC
— серединный перпендикуляр к отрезку BD
. Из равенства \frac{1}{2}AC\cdot BD=12
(площадь четырёхугольника ABCD
) находим, что
BD=\frac{2\cdot12}{AC}=\frac{2\cdot12}{5}=\frac{24}{5}.
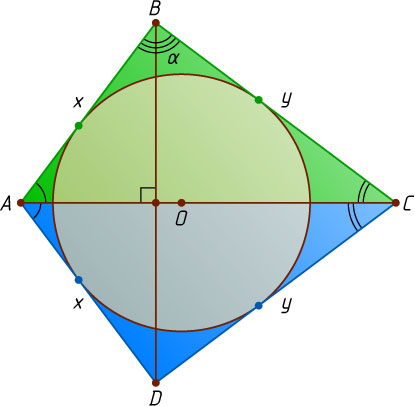
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — Диагностическая работа 1, задача 6
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 6, с. 164
