3318. Биссектрисы внутренних углов треугольника продолжены до пересечения с описанной около треугольника окружностью. В результате попарного соединения этих точек получился новый треугольник. Известно, что углы исходного треугольника равны 30^{\circ}
, 60^{\circ}
и 90^{\circ}
, а его площадь равна 2. Найдите площадь нового треугольника.
Ответ. 1+\sqrt{3}
.
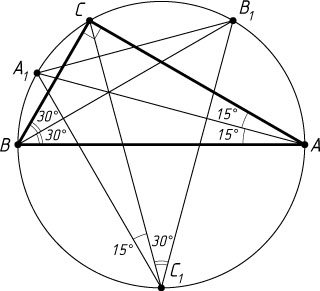
Решение. Пусть биссектрисы углов при вершинах A
, B
и C
треугольника ABC
пересекают описанную около треугольника окружность радиуса R
в точках A_{1}
, B_{1}
и C_{1}
соответственно, причём \angle C=90^{\circ}
, \angle A=30^{\circ}
и \angle B=60^{\circ}
.
Тогда
\angle C_{1}=\angle CC_{1}B_{1}+\angle CC_{1}A_{1}=\angle CAA_{1}+\angle CBB_{1}=15^{\circ}+30^{\circ}=45^{\circ}.
Аналогично находим, что
\angle A_{1}=30^{\circ}+45^{\circ}=75^{\circ},~\angle B_{1}=45^{\circ}+15^{\circ}=60^{\circ}.
По условию задачи S_{\triangle ABC}=2
, или 2R^{2}\sin A\sin B\sin C=2
, откуда находим, что
R^{2}=\frac{2}{2\sin A\sin B\sin C}=\frac{1}{\sin30^{\circ}\sin60^{\circ}\sin90^{\circ}}=\frac{4}{\sqrt{3}}.
Следовательно,
S_{\triangle A_{1}B_{1}C_{1}}=2R^{2}\sin A_{1}\sin B_{1}\sin C_{1}=2R^{2}\sin75^{\circ}\sin60^{\circ}\sin45^{\circ}=
=\frac{8}{\sqrt{3}}\cdot\frac{\sqrt{6}+\sqrt{2}}{4}\cdot\frac{\sqrt{3}}{2}\cdot\frac{\sqrt{2}}{2}=\sqrt{3}+1.
Источник: Вступительный экзамен на факультет почвоведения МГУ. — 2000 (июль), вариант 1, № 6
Источник: Вступительные экзамены и олимпиады по математике 2000—2002 гг. / Под общ. ред. И. Н. Сергеева. — М.: Изд-во ЦПИ при мехмате МГУ, 2003. — с. 180
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — Диагностическая работа 4, задача 6
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 6, с. 167
