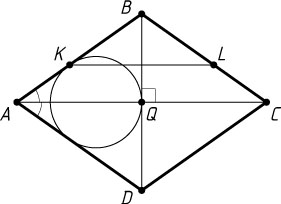
3319. Площадь ромба ABCD
равна 2. В треугольник ABD
вписана окружность, которая касается стороны AB
в точке K
. Через точку K
проведена прямая KL
, параллельная диагонали AC
ромба (точка L
лежит на стороне BC
). Известно, что площадь треугольника KLB
равна \frac{1}{3}
. Найдите косинус угла BAD
.
Ответ. \frac{1}{3}
.
Указание. Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Решение. Треугольник KBL
подобен треугольнику ABC
с коэффициентом \frac{\sqrt{S_{\triangle KBL}}}{\sqrt{S_{\triangle ABC}}}=\frac{\frac{1}{\sqrt{3}}}{1}=\frac{1}{\sqrt{3}}
, поэтому, если Q
— точка пересечения диагоналей ромба, то
\sin\angle BAC=\sin\angle BAQ=\frac{BQ}{AB}=\frac{BK}{AB}=\frac{1}{\sqrt{3}}.
Следовательно,
\cos\angle BAD=1-2\sin^{2}\angle BAC=1-2\cdot\frac{1}{3}=\frac{1}{3}.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — Диагностическая работа 5, задача 6
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 6, с. 168
