3320. Точка M
делит среднюю линию треугольника ABC
, параллельную стороне BC
, на отрезки, один из которых в три раза длиннее другого. Точка N
делит сторону BC
на отрезки, один из которых в три раза длиннее другого. В каком отношении прямая MN
делит площадь треугольника ABC
?
Ответ. \frac{1}{3}
или \frac{9}{11}
.
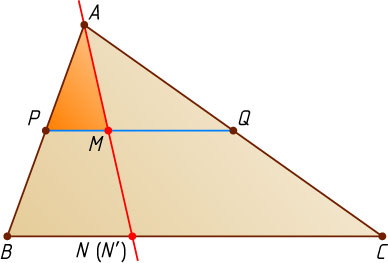
Решение. Пусть P
и Q
— середины сторон AB
и AC
соответственно, точка M
лежит на средней линии PQ
, причём PM:MQ=1:3
, а прямая AM
пересекает сторону BC
в точке N'
(рис. 1).
Треугольник APM
подобен треугольнику ABN'
с коэффициентом \frac{AP}{AB}=\frac{1}{2}
, а треугольник APQ
подобен треугольнику ABC
с тем же коэффициентом, поэтому \frac{PM}{BN'}=\frac{PQ}{BC}
. Значит, \frac{BN'}{BC}=\frac{PM}{PQ}=\frac{1}{4}
и \frac{BN'}{N'C}=\frac{1}{3}
. Следовательно, в этом случае точка N'
совпадает с точкой N
, о которой говорится в условии задачи. Тогда
\frac{S_{\triangle ABN}}{S_{\triangle ACN}}=\frac{BN}{NC}=\frac{1}{3}.
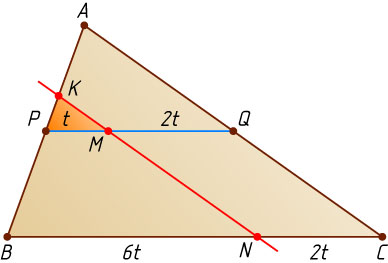
Пусть теперь \frac{CN}{NB}=\frac{1}{3}
(рис. 2). В этом случае прямая MN
пересекает сторону AB
в некоторой точке K
. Обозначим PM=t
. Тогда PQ=4t
, BC=8t
, BN=6t
. Треугольник KPM
подобен треугольнику KBN
с коэффициентом \frac{PM}{BN}=\frac{t}{6t}=\frac{1}{6}
, значит,
BK=6KP,~AP=BP=5KP,~AK=AP-KP=5KP-KP=4KP,
\frac{BK}{AK}=\frac{6KP}{4KP}=\frac{3}{2},~\frac{BK}{AB}=\frac{3}{5}.
Следовательно,
\frac{S_{\triangle BKN}}{S_{\triangle ABC}}=\frac{BN}{BC}\cdot\frac{BK}{AB}=\frac{3}{4}\cdot\frac{3}{5}=\frac{9}{20},~\frac{S_{\triangle BKN}}{S_{ACNK}}=\frac{9}{11}.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — Диагностическая работа 5, задача 5
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 5, с. 168

