3321. В треугольнике ABC
известно, что AB=18
, BC=16
, \cos\angle B=\frac{4}{9}
, AH
— высота. Через точку H
, проведена прямая, отсекающая от треугольника подобный ему треугольник и пересекающая сторону AB
в точке M
. Найдите HM
.
Ответ. 9
или 8
.
Решение. По теореме косинусов
AC=\sqrt{AB^{2}+BC^{2}-2AB\cdot BC\cos\angle B}=\sqrt{18^{2}+16^{2}-2\cdot18\cdot16\cdot\frac{4}{9}}=18,
поэтому треугольник ABC
равнобедренный с основанием BC
, значит, H
— середина BC
.
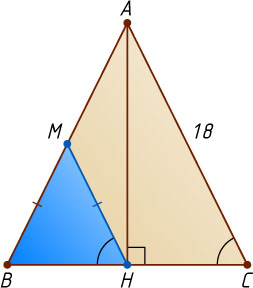
Заметим, что существует ровно два случая расположения точки M
на стороне AB
: либо \angle BHM=\angle BCA
(рис. 1), либо \angle BHM=\angle BAC
(рис. 2).
В первом из этих случаев HM\parallel BC
. Тогда HM
— средняя линия треугольника ABC
, следовательно, HM=\frac{1}{2}AC=9
.
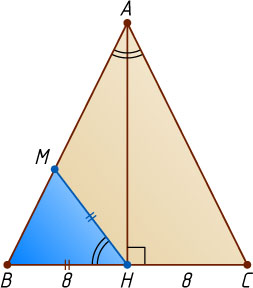
Пусть теперь \angle BHM=\angle BAC
. Тогда треугольник BAM
подобен равнобедренному треугольнику BAC
, следовательно,
HM=HB=\frac{1}{2}BC=8.
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 1, с. 159
Источник: Диагностические и тренировочные задачи ЕГЭ. — Задача C4, 2010 г.

