3325. Расстояние между центрами окружностей радиусов 1 и 9 равно 17. Этих окружностей и их общей внешней касательной касается третья окружность. Найдите её радиус.
Ответ. \frac{225}{64}
, \frac{225}{16}
, \frac{25}{4}
или \frac{225}{4}
.
Решение. Докажем сначала следующее утверждение. Если a
— расстояние между центрами окружностей радиусов r
и R
, общая внешняя касательная касается этих окружностей соответственно в точках A
и B
и при этом a\geqslant r+R
, то AB=\sqrt{a^{2}-(R-r)^{2}}
.
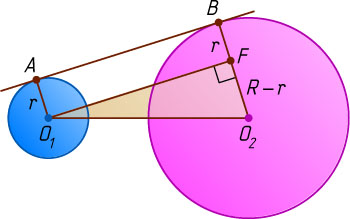
Действительно, пусть O_{1}
и O_{2}
— центры окружностей радиусов r
и R
соответственно (рис. 1). Из точки O_{1}
опустим перпендикуляр O_{1}F
на прямую O_{2}B
. Из прямоугольного треугольника O_{1}FO_{2}
находим, что
O_{1}F=\sqrt{O_{1}O_{2}^{2}-FO_{2}^{2}}=\sqrt{a^{2}-(R-r)^{2}}.
Следовательно, AB=O_{1}F=\sqrt{a^{2}-(R-r)^{2}}
. Утверждение доказано.
В частности, если окружности касаются внешним образом, то a=R+r
. В этом случае
AB=\sqrt{(R+r)^{2}-(R-r)^{2}}=2\sqrt{Rr}.
Пусть x
— радиус искомой окружности, C
— её точка касания с прямой AB
. По доказанному
AB=\sqrt{17^{2}-(9-1)^{2}}=15,
AC=\sqrt{(x+1)^{2}-(x-1)^{2}}=2\sqrt{x},~BC=\sqrt{(x+9)^{2}-(x-9)^{2}}=2\sqrt{9x}=6\sqrt{x}.
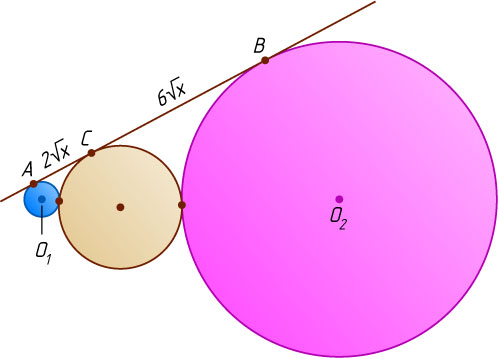
Если искомая окружность касается прямой AB
в точке C
, лежащей между A
и B
(рис. 2), то AC+CB=AB
, или 2\sqrt{x}+6\sqrt{x}=15
. Тогда \sqrt{x}=\frac{15}{8}
. Следовательно, x=\frac{225}{64}
.
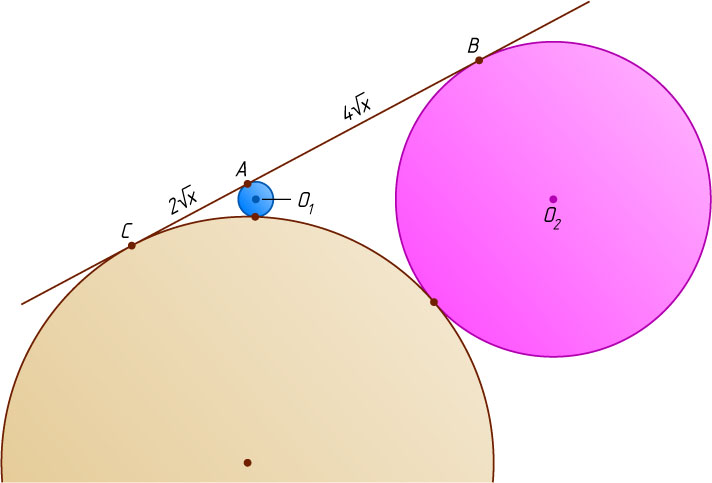
Если искомая окружность касается прямой AB
в точке C
, лежащей на продолжении отрезка AB
(рис. 3), то CB-AC=AB
, или 6\sqrt{x}-2\sqrt{x}=15
. Тогда \sqrt{x}=\frac{15}{4}
. Следовательно, x=\frac{225}{16}
.
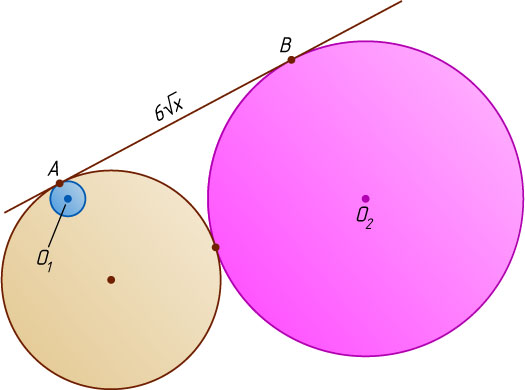
Пусть искомая окружность радиуса x
касается прямой AB
, внутренним образом касается окружности с центром O_{1}
в точке A
, а внешним образом — окружности с центром O_{2}
(рис. 4). Тогда AB=2\sqrt{9x}
, или 15=6\sqrt{x}
, откуда находим, что x=\frac{25}{4}
.
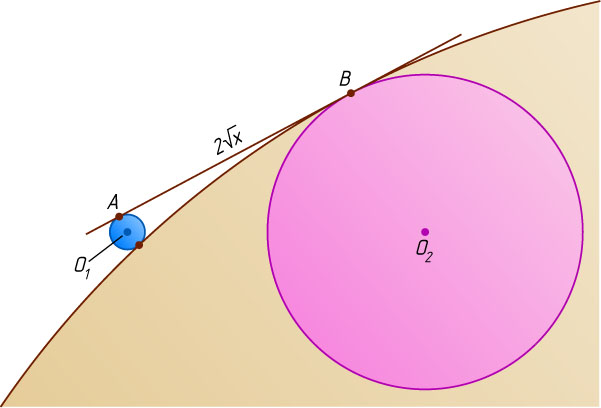
Наконец, если искомая окружность радиуса x
касается прямой AB
, внутренним образом касается окружности с центром O_{2}
в точке B
, а внешним образом — окружности с центром O_{1}
(рис. 5), то аналогично получим уравнение 15=2\sqrt{1\cdot x}
, из которого находим, что x=\frac{225}{4}
.
Источник: Диагностические и тренировочные задачи ЕГЭ. — Задача C4, 2010 г.
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 5, с. 160




