3326. Расстояние между центрами окружностей радиусов 1 и 9 равно 17. Этих окружностей и их общей внутренней касательной касается третья окружность. Найдите её радиус.
Ответ. \frac{21}{4}
или \frac{189}{4}
.
Решение. Докажем сначала следующее утверждение. Если a
— расстояние между центрами окружностей радиусов r
и R
, a\geqslant r+R
, общая внешняя касательная касается окружностей в точках A
и B
, общая внутренняя — в точках C
и D
, то
AB=\sqrt{a^{2}-(R-r)^{2}},~CD=\sqrt{a^{2}-(R+r)^{2}}.
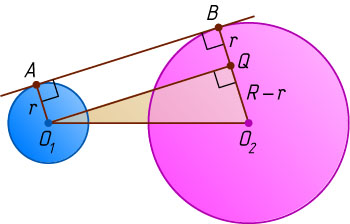
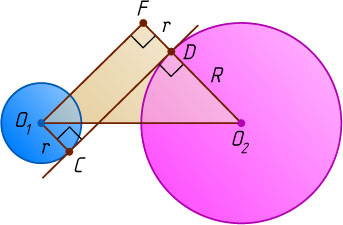
Действительно, пусть O_{1}
и O_{2}
— центры окружностей радиусов r
и R
соответственно (рис. 1). Из точек O_{1}
и O_{2}
опустим перпендикуляры O_{1}Q
на прямую O_{2}B
и O_{2}F
на прямую O_{1}C
. Из прямоугольных треугольников O_{1}QO_{2}
и O_{1}FO_{2}
находим, что
O_{1}Q=\sqrt{O_{1}O_{2}^{2}-QO_{2}^{2}}=\sqrt{a^{2}-(R-r)^{2}},
O_{1}F=\sqrt{O_{1}O_{2}^{2}-FO_{1}^{2}}=\sqrt{a^{2}-(R+r)^{2}}.
Следовательно, CD=O_{1}Q=\sqrt{a^{2}-(R+r)^{2}}
.
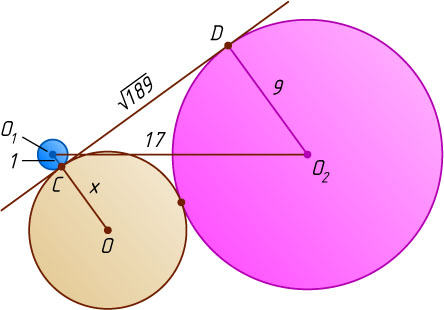
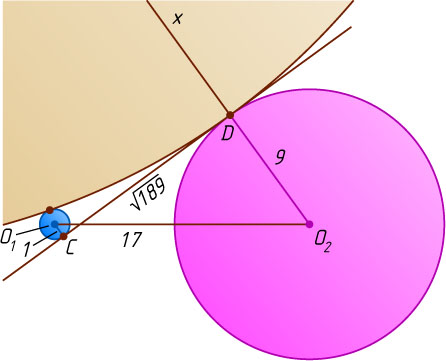
Пусть x
— радиус искомой окружности, O
— её центр. Заметим, что прямая CD
— общая внешняя касательная либо окружностей с центрами O
и O_{2}
(рис. 2), либо окружностей с центрами O
и O_{1}
(рис. 3). В первом из этих случаев искомая окружность касается прямой CD
в точке C
, во втором — в точке D
.
По доказанному
CD=\sqrt{17^{2}-(9+1)^{2}}=\sqrt{189}.
В первом случае CD
— общая внешняя касательная к окружностям с центрами O
и O_{2}
, поэтому
CD=\sqrt{(x+9)^{2}-(9-x)^{2}}=2\sqrt{9x},
значит, 2\sqrt{9x}=\sqrt{189}
. Следовательно, x=\frac{21}{4}
.
Во втором случае CD
— общая внешняя касательная к окружностям с центрами O
и O_{1}
, поэтому
CD=\sqrt{(x+1)^{2}-(x-1)^{2}}=2\sqrt{x},
значит, 2\sqrt{x}=\sqrt{189}
. Следовательно, x=\frac{189}{4}
.
Источник: Диагностические и тренировочные задачи ЕГЭ. — Задача C4, 2010 г.
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 6, с. 163



