3328. Площадь трапеции ABCD
равна 405. Диагонали пересекаются в точке O
, отрезки, соединяющие середину P
основания AD
с вершинами B
и C
, пересекаются с диагоналями трапеции в точках M
и N
. Найдите площадь треугольника MON
, если одно из оснований трапеции вдвое больше другого.
Ответ. \frac{45}{8}
или \frac{36}{5}
.
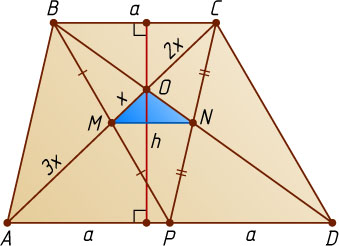
Решение. Пусть AD=2BC
(рис. 1). Четырёхугольники ABCP
и BCDP
— параллелограммы, поэтому M
и N
— середины BP
и CP
, значит, CM
и BN
— медианы треугольника BPC
. Пусть h
— высота трапеции. Положим BC=a
, AD=2a
, OM=x
. Тогда
\frac{a+2a}{2}h=\frac{3}{2}ah=405,~ah=270,~S_{\triangle BPC}=\frac{1}{2}\cdot2a\cdot h=ah=135,
а так как O
— точка пересечения медиан треугольника BPC
, то OC=2x
, поэтому
AM=MC=3x,~OA=AM+OM=3x+x=4x,~\frac{OM}{OA}=\frac{x}{4x}=\frac{1}{4}.
Аналогично, \frac{ON}{OD}=\frac{1}{4}
, значит, треугольник MON
подобен треугольнику AOD
с коэффициентом \frac{1}{4}
. Следовательно,
S_{\triangle MON}=\left(\frac{1}{4}\right)^{2}\cdot S_{\triangle AOD}=\frac{1}{16}\cdot\frac{1}{2}\cdot2a\cdot\frac{2}{3}h=\frac{1}{24}ah=\frac{1}{24}\cdot135=\frac{45}{8}.
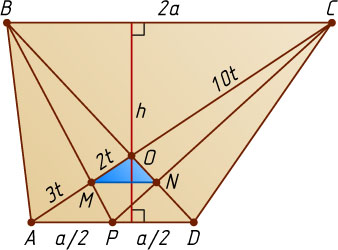
Рассмотрим случай, когда BC=2AD
(рис. 2). Пусть h
— высота трапеции. Положим AD=a
, BC=2a
, AM=3t
. Тогда ah=270
.
Треугольник AOD
подобен треугольнику COB
с коэффициентом \frac{1}{2}
, а треугольник AMP
— треугольнику CMB
с коэффициентом \frac{AP}{BC}=\frac{1}{4}
. Тогда
\frac{AM}{MC}=\frac{1}{4},~\frac{PM}{PB}=\frac{1}{5},~MC=12t,~AC=AM+MC=15t,~AO=5t,~MO=2t,
значит, \frac{OM}{OA}=\frac{2t}{5t}=\frac{2}{5}
. Аналогично, \frac{ON}{OD}=\frac{2}{5}
. Следовательно,
S_{\triangle MON}=\left(\frac{2}{5}\right)^{2}\cdot S_{\triangle AOD}=\frac{4}{25}\cdot\frac{1}{2}a\cdot\frac{1}{3}h=\frac{2}{75}ah=\frac{2}{75}\cdot270=\frac{36}{5}.
Источник: Диагностические и тренировочные задачи ЕГЭ. — Задача C4, 2010 г.
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 8, с. 165

