3334. В параллелограмме ABCD
биссектрисы углов при стороне AD
делят сторону BC
точками M
и N
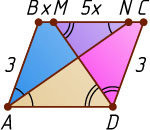
так, что BM:MN=1:5
. Найдите BC
, если AB=3
.
Ответ. 21 или 3,5.
Решение. Положим BM=x
, MN=5x
. Точка M
лежит между точками B
и N
, так как BM\lt MN
.
Рассмотрим случай, когда AM
и DN
— биссектрисы углов при вершинах A
и D
параллелограмма ABCD
(рис. 1).
Треугольник ABM
— равнобедренный, так как \angle AMB=\angle MAD=\angle BAM
, поэтому BM=AB=3
, т. е. x=3
. Тогда MN=5x=15
. Аналогично, треугольник DCN
— также равнобедренный и CN=CD=AB=3
. Следовательно,
BC=BM+MN+CN=3+15+3=21.
Пусть теперь биссектрисы углов при основании AD
— это лучи AN
и DM
(рис. 2). Тогда треугольники ABN
и DCN
— равнобедренные, CM=CD=AB=3
, BN=BM+MN=x+5x=6x
и BN=AB=3
. Из равенства 6x=3
находим, что x=\frac{1}{2}
. Следовательно,
BC=BM+CM=x+3=\frac{1}{2}+3=\frac{7}{2}.

Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 14, с. 168

