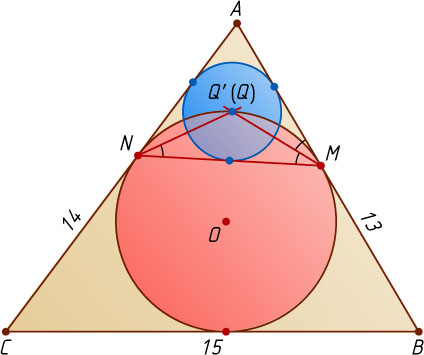
3336. Окружность с центром O
, вписанная в треугольник ABC
, касается его сторон AB
и AC
в точках M
и N
. Окружность с центром Q
вписана в треугольник AMN
. Найдите OQ
, если AB=13
, BC=15
и AC=14
.
Ответ. 4.
Решение. Пусть r
— радиус окружности, вписанной в треугольник ABC
, p
— полупериметр треугольника ABC
. Тогда
p=\frac{AB+BC+AC}{2}=\frac{13+14+15}{2}=21.
По формуле Герона
S_{\triangle ABC}=\sqrt{p(p-AB)(p-BC)(p-AC)}=\sqrt{21\cdot8\cdot6\cdot7}=84,
значит,
r=\frac{S_{\triangle ABC}}{p}=\frac{84}{21}=4.
Докажем, что центр Q
окружности, вписанной в треугольник AMN
, лежит на вписанной окружности треугольника ABC
. Действительно, пусть Q'
— середина меньшей дуги MN
вписанной окружности треугольника ABC
. Из теоремы об угле между касательной и хордой следует, что
\angle AMQ'=\angle MNQ'=\angle NMQ',
поэтому MQ'
— биссектриса угла AMN
. Аналогично, NQ'
— биссектриса угла ANM
, значит, Q'
— точка пересечения биссектрис треугольника AMN
, т. е. центр вписанной окружности этого треугольника. Таким образом, точка Q'
совпадает с точкой Q
.
Следовательно, OQ=r=4
.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — Диагностическая работа 4, задача 5
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 5, с. 167
