3337. Окружности радиусов r
и R
касаются внешним образом в точке K
. Прямая касается этих окружностей в различных точках A
и B
. Найдите площадь треугольника AKB
.
Ответ. \frac{2Rr\sqrt{rR}}{r+R}
.
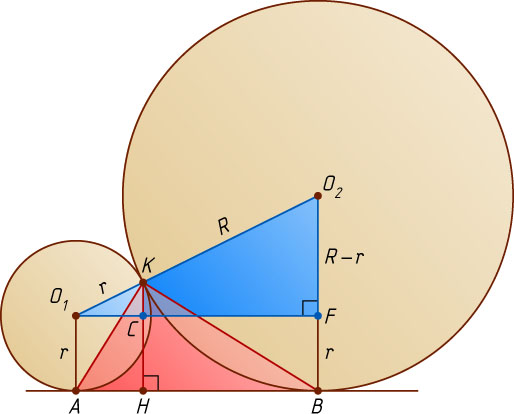
Решение. Пусть прямая AB
касается окружности радиуса r
с центром O_{1}
в точке A
, окружности радиуса R
с центром O_{2}
— в точке B
, KH
— высота треугольника ABK
, F
— проекция точки O_{1}
на O_{2}B
, C
— точка пересечения KH
и O_{1}F
.
Линия центров двух касающихся окружностей проходит через точку их касания, поэтому точки O_{1}
, K
и O_{2}
лежат на одной прямой. Прямые O_{1}A
, KH
и O_{2}B
параллельны, так как они перпендикулярны одной и той же прямой AB
. Треугольник KO_{1}C
подобен треугольнику O_{2}O_{1}F
с коэффициентом \frac{O_{1}K}{O_{1}O_{2}}=\frac{r}{R+r}
, поэтому
CK=O_{2}F\cdot\frac{r}{R+r}=(R-r)\cdot\frac{r}{R+r}=\frac{r(R-r)}{R+r},
значит,
KH=CK+CH=CK+O_{1}A=\frac{r(R-r)}{R+r}+r=\frac{2rR}{R+r}.
Из прямоугольного треугольника O_{1}O_{2}F
находим, что
O_{1}F=\sqrt{O_{1}O_{2}^{2}-O_{2}F^{2}}=\sqrt{(R+r)^{2}-(R-r)^{2}}=2\sqrt{rR},
значит, AB=O_{1}F=2\sqrt{rR}
. Следовательно,
S_{\triangle AKB}=\frac{1}{2}AB\cdot KH=\frac{1}{2}\cdot2\sqrt{rR}\cdot\frac{2rR}{R+r}=\frac{2Rr\sqrt{rR}}{r+R}.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — Диагностическая работа 5, задача 3
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 3, с. 168
