3338. Один из смежных углов с вершиной A
вдвое больше другого. В эти углы вписаны окружности с центрами O_{1}
и O_{2}
. Найдите углы треугольника O_{1}AO_{2}
, если отношение радиусов окружностей равно \sqrt{3}
.
Ответ. 90^{\circ}
, 45^{\circ}
, 45^{\circ}
или 90^{\circ}
, \arctg3
, \arcctg3
.
Решение. Один из смежных углов равен 60^{\circ}
, а второй — 120^{\circ}
.
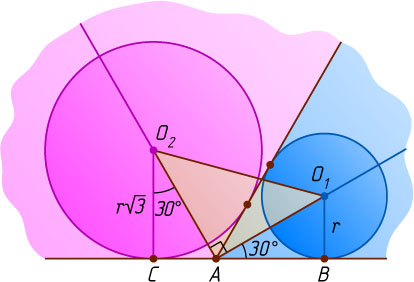
Пусть окружность с центром O_{1}
радиуса r
вписана в угол, равный 60^{\circ}
, а окружность с центром O_{2}
радиуса r\sqrt{3}
— в угол, равный 120^{\circ}
(рис. 1), причём окружности касаются прямой, содержащей дополнительные стороны этих углов, в точках B
и C
соответственно.
Центр окружности, вписанной в угол, лежит на биссектрисе угла, поэтому
\angle O_{1}AB=30^{\circ},~\angle O_{2}AC=60^{\circ},~\angle O_{1}AO_{2}=90^{\circ}.
Из прямоугольных треугольников O_{1}AB
и O_{2}AC
находим, что
AO_{1}=2O_{1}B=2r,~AO_{2}=\frac{O_{2}C}{\sin60^{\circ}}=\frac{r\sqrt{3}}{\frac{\sqrt{3}}{2}}=2r.
Треугольник O_{1}AO_{2}
— прямоугольный и равнобедренный, следовательно, его острые углы равны по 45^{\circ}
.
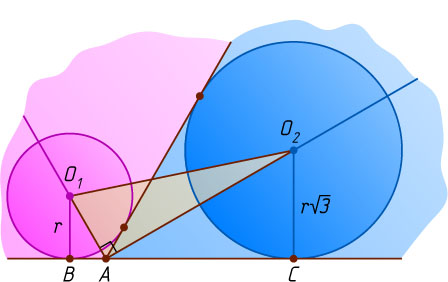
Пусть теперь окружность с центром O_{1}
радиуса r
вписана в угол, равный 120^{\circ}
, а окружность с центром O_{2}
радиуса r\sqrt{3}
— в угол, равный 60^{\circ}
(рис. 2), причём окружности касаются прямой, содержащей дополнительные стороны этих углов, в точках B
и C
соответственно. Из прямоугольных треугольников O_{1}AB
и O_{2}AC
находим, что
AO_{1}=\frac{O_{1}B}{\sin60^{\circ}}=\frac{2r}{\sqrt{3}},~AO_{2}=2O_{2}C=2r\sqrt{3}.
Следовательно,
\tg\angle AO_{1}O_{2}=\frac{AO_{2}}{AO_{1}}=\frac{2r\sqrt{3}}{\frac{2r}{\sqrt{3}}}=3,~\tg\angle AO_{2}O_{1}=\frac{1}{3}.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 8.23, с. 62

