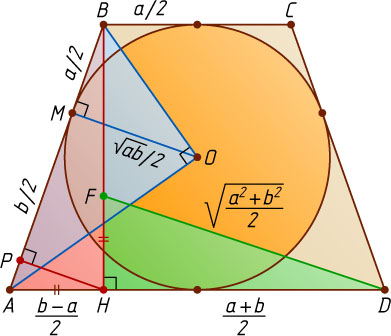
3341. Геометрический смысл классических неравенств. Окружность вписана в равнобедренную трапецию ABCD
с основаниями BC=a
и AD=b
. Точка H
— проекция вершины B
на AD
, точка P
— проекция точки H
на AB
, точка F
лежит на отрезке BH
, причём FH=AH
. Найдите AB
, BH
, BP
, DF
и расположите найденные величины по возрастанию.
Ответ. BP=\frac{2ab}{a+b}
, BH=\sqrt{ab}
, AB=\frac{a+b}{2}
, DF=\sqrt{\frac{a^{2}+b^{2}}{2}}
.
Решение. Рассмотрим случай a\lt b
.
Если в четырёхугольник вписана окружность, то суммы его противоположных сторон равны, поэтому AB+CD=BC+AD=a+b
, а так как AB=CD
, то 2AB=a+b
, следовательно, AB=\frac{a+b}{2}
.
Пусть O
— центр окружности радиуса r
, вписанной в трапецию ABCD
, M
— точка касания окружности с боковой стороной AB
. Тогда BM=\frac{1}{2}BC=\frac{a}{2}
, AM=\frac{1}{2}AD=\frac{b}{2}
. Отрезок OM
— высота прямоугольного треугольника AOB
, проведённая из вершины прямого угла, поэтому
r=OM=\sqrt{BM\cdot AM}=\sqrt{\frac{a}{2}\cdot\frac{b}{2}}=\frac{\sqrt{ab}}{2}.
Следовательно, BH=2r=\sqrt{ab}
.
Отрезок HP
— высота прямоугольного треугольника AHB
, проведённая из вершины прямого угла, поэтому
BP=\frac{HP^{2}}{AB}=\frac{ab}{\frac{a+b}{2}}=\frac{2ab}{a+b}.
Поскольку трапеция ABCD
равнобедренная,
AH=\frac{AD-BC}{2}=\frac{b-a}{2},~DH=\frac{AD+BC}{2}=\frac{b+a}{2}.
Из прямоугольного треугольника DFH
по теореме Пифагора находим, что
DF=\sqrt{DH^{2}+FH^{2}}=\sqrt{AB^{2}+AH^{2}}=\sqrt{\left(\frac{a+b}{2}\right)^{2}+\left(\frac{b-a}{2}\right)^{2}}=\sqrt{\frac{a^{2}+b^{2}}{2}}.
BP
— катет прямоугольного треугольника BPH
с гипотенузой BH
, поэтому BP\lt BH
.
BH
— катет прямоугольного треугольника ABH
с гипотенузой AB
, поэтому BH\lt AB
.
DH
— катет прямоугольного треугольника DFH
с гипотенузой DF
, поэтому AB=DH\lt DF
.
Следовательно, BP\lt BH\lt AB\lt DF
, или
\frac{2ab}{a+b}\lt\sqrt{ab}\lt\frac{a+b}{2}\lt\sqrt{\frac{a^{2}+b^{2}}{2}}.
Аналогично для a\gt b
.
Примечание. 1. Число \frac{a+b}{2}
называется средним арифметическим чисел a
и b
,
\sqrt{ab}
— средним геометрическим чисел a
и b
,
\frac{2ab}{a+b}
— средним гармоническим чисел a
и b
,
\sqrt{\frac{a^{2}+b^{2}}{2}}
— средним квадратичным (средним квадратическим) чисел a
и b
.
Для любых двух неотрицательных чисел a
и b
верно неравенство
\frac{2ab}{a+b}\leqslant\sqrt{ab}\leqslant\frac{a+b}{2}\leqslant\sqrt{\frac{a^{2}+b^{2}}{2}},
причём равенство достигается тогда и только тогда, когда a=b
.
2. Число \frac{a_{1}+a_{2}+\dots+a_{n}}{n}
называется средним арифметическим чисел a_{1}
, a_{2}
, …, a_{n}
;
\sqrt[{n}]{{a_{1}a_{2}\dots a_{n}}}
— средним геометрическим чисел a_{1}
, a_{2}
, …, a_{n}
;
\frac{n}{\frac{1}{a_{1}}+\frac{1}{a_{2}}+\dots+\frac{1}{a_{n}}}
— средним гармоническим чисел a_{1}
, a_{2}
, …, a_{n}
;
\sqrt{\frac{a_{1}^{2}+a_{2}^{2}+\dots+a_{n}^{2}}{n}}
— средним квадратичным (средним квадратическим) чисел a_{1}
, a_{2}
, …, a_{n}
.
Для любых положительных чисел a_{1}
, a_{2}
, …, a_{n}
верно неравенство
\frac{n}{\frac{1}{a_{1}}+\frac{1}{a_{2}}+\dots+\frac{1}{a_{n}}}\leqslant\sqrt[{n}]{{a_{1}a_{2}\dots a_{n}}}\leqslant\frac{a_{1}+a_{2}+\dots+a_{n}}{n}\leqslant\sqrt{\frac{a_{1}^{2}+a_{2}^{2}+\dots+a_{n}^{2}}{n}},
причём равенство достигается тогда и только тогда, когда a_{1}=a_{2}=\dots=a_{n}
.
3. См. также статью А.Гольдмана и Л.Звавича «Числовые средние и геометрия», Квант, 1990, N9, с.62-65.
4. См. также статью Л.Шибасова «Соотношения между средними величинами», Квант, 2004, N4, с.42-46.
