3342. Геометрический смысл классических неравенств. Основания BC
и AD
трапеции ABCD
равны a
и b
. Проведены четыре прямые, параллельные основаниям. Первая проходит через середины боковых сторон, вторая — через точку пересечения диагоналей трапеции, третья разбивает трапецию на две подобные, четвёртая — на две равновеликие. Найдите отрезки этих прямых, заключённые внутри трапеции, и расположите найденные величины по возрастанию.
Ответ. \frac{2ab}{a+b}
, \sqrt{ab}
, \frac{a+b}{2}
, \sqrt{\frac{a^{2}+b^{2}}{2}}
.
Решение. Для определённости будем считать, что BC=a\lt b=AD
.
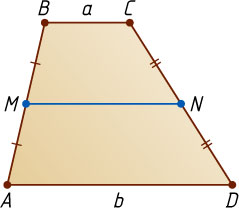
Пусть M
и N
— середины боковых сторон трапеции (рис. 1). Тогда MN
— её средняя линия, следовательно,
MN=\frac{BC+AD}{2}=\frac{a+b}{2}.
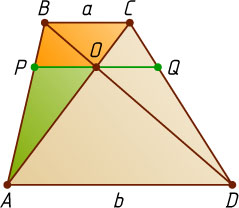
Пусть прямая, параллельная основаниям трапеции, проходит через точку O
пересечения диагоналей и пересекает боковые стороны AB
и CD
в точках P
и Q
соответственно (рис. 2). Треугольник AOD
подобен треугольнику COB
с коэффициентом \frac{AD}{BC}=\frac{b}{a}
, а треугольник AOP
подобен треугольнику ACB
с коэффициентом \frac{AO}{AC}=\frac{b}{a+b}
, значит,
OP=\frac{b}{a+b}\cdot BC=\frac{b}{a+b}\cdot a=\frac{ab}{a+b}.
Аналогично, OQ=\frac{ab}{a+b}
. Следовательно, PQ=\frac{2ab}{a+b}
.
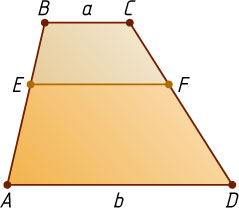
Пусть прямая, параллельная основаниям, пересекает боковые стороны AB
и CD
трапеции в точках E
и F
соответственно (рис. 3) и при этом трапеция BEFC
подобна трапеции EADF
. Тогда \frac{BC}{EF}=\frac{EF}{AD}
, значит,
EF^{2}=BC\cdot AD=ab.
Следовательно, EF=\sqrt{ab}
.
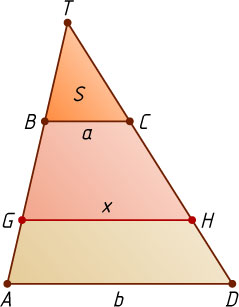
Пусть прямая, параллельная основаниям, пересекает боковые стороны AB
и CD
трапеции в точках G
и H
(рис. 4) соответственно и при этом трапеции BGHC
и AGHD
равновелики.
Обозначим GH=x
. Если прямые AB
и CD
пересекаются в точке T
, то треугольник TGH
подобен треугольнику TBC
с коэффициентом \frac{GH}{BC}=\frac{x}{a}
, треугольник TAD
подобен треугольнику TBC
с коэффициентом \frac{AD}{BC}=\frac{b}{a}
.
Обозначим S_{\triangle TBC}=S
. Тогда
S_{\triangle TGH}=\left(\frac{x}{a}\right)^{2}S,~S_{\triangle TAD}=\left(\frac{b}{a}\right)^{2}S,
S_{BGHC}=S_{\triangle TGH}-S_{\triangle TBC}=\left(\frac{x}{a}\right)^{2}S-S,~S_{AGHD}=S_{\triangle TAD}-S_{\triangle TGH}=\left(\frac{b}{a}\right)^{2}S-\left(\frac{x}{a}\right)^{2}S.
Из уравнения \left(\frac{x}{a}\right)^{2}S-S=\left(\frac{b}{a}\right)^{2}S-\left(\frac{x}{a}\right)^{2}S
находим, что x=\sqrt{\frac{a^{2}+b^{2}}{2}}
.
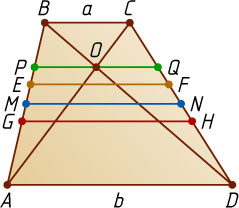
На чертеже видно (рис. 5), что самый близкий к меньшему основанию — отрезок PQ
, затем EF
, MN
и GH
. Соответствующие неравенства
\frac{2ab}{a+b}\lt\sqrt{ab}\lt\frac{a+b}{2}\lt\sqrt{\frac{a^{2}+b^{2}}{2}}
легко доказать аналитически.
Примечание. 1. Число \frac{a+b}{2}
называется средним арифметическим чисел a
и b
,
\sqrt{ab}
— средним геометрическим чисел a
и b
,
\frac{2ab}{a+b}
— средним гармоническим чисел a
и b
,
\sqrt{\frac{a^{2}+b^{2}}{2}}
— средним квадратичным (средним квадратическим) чисел a
и b
.
Для любых двух неотрицательных чисел a
и b
верно неравенство
\frac{2ab}{a+b}\leqslant\sqrt{ab}\leqslant\frac{a+b}{2}\leqslant\sqrt{\frac{a^{2}+b^{2}}{2}},
причём равенство достигается тогда и только тогда, когда a=b
(в нашем случае трапеция вырождается в параллелограмм).
2. Число \frac{a_{1}+a_{2}+\dots+a_{n}}{n}
называется средним арифметическим чисел a_{1}
, a_{2}
, …, a_{n}
;
\sqrt[{n}]{{a_{1}a_{2}\dots a_{n}}}
— средним геометрическим чисел a_{1}
, a_{2}
, …, a_{n}
;
\frac{n}{\frac{1}{a_{1}}+\frac{1}{a_{2}}+\dots+\frac{1}{a_{n}}}
— средним гармоническим чисел a_{1}
, a_{2}
, …, a_{n}
;
\sqrt{\frac{a_{1}^{2}+a_{2}^{2}+\dots+a_{n}^{2}}{n}}
— средним квадратичным (средним квадратическим) чисел a_{1}
, a_{2}
, …, a_{n}
.
Для любых положительных чисел a_{1}
, a_{2}
, …a_{n}
; верно неравенство
\frac{n}{\frac{1}{a_{1}}+\frac{1}{a_{2}}+\dots+\frac{1}{a_{n}}}\leqslant\sqrt[{n}]{{a_{1}a_{2}\dots a_{n}}}\leqslant\frac{a_{1}+a_{2}+\dots+a_{n}}{n}\leqslant\sqrt{\frac{a_{1}^{2}+a_{2}^{2}+\dots+a_{n}^{2}}{n}},
причём равенство достигается тогда и только тогда, когда a_{1}=a_{2}=\dots=a_{n}
.
3. См. также статью А.Гольдмана и Л.Звавича «Числовые средние и геометрия», Квант, 1990, N9, с.62-65.
4. См. также статью Л.Шибасова «Соотношения между средними величинами», Квант, 2004, N4, с.42-46.




