3343. Точка C
— середина отрезка AB
. На произвольном луче, проведённом из точки C
и не лежащем на прямой AB
, выбраны три точки P
, M
и Q
так, что PM=MQ
. Докажите, что AP+BQ\gt2CM
.
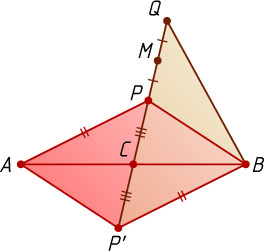
Решение. На продолжении отрезка PC
за точку C
отложим отрезок CP'
, равный CP
. Диагонали четырёхугольника APBP'
точкой пересечения C
делятся пополам, значит, это параллелограмм, поэтому AP=P'B
. По неравенству треугольника
AP+BQ=P'B+BQ\gt P'Q=PP'+PQ=2CP+2PM=2(CP+PM)=2CM.
Что и требовалось доказать.
