3345. Сумма расстояний между серединами противоположных сторон четырёхугольника равна его полупериметру. Докажите, что этот четырёхугольник — параллелограмм.
Решение. Первый способ. Пусть K
, L
, M
, N
— середины сторон соответственно AB
, BC
, CD
, AD
четырёхугольника ABCD
.
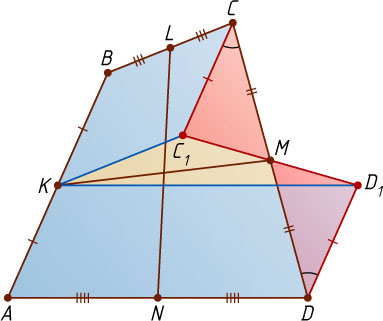
Предположим, что прямые BC
и AD
не параллельны. Пусть C_{1}
и D_{1}
— вершины параллелограммов KBCC_{1}
и AKD_{1}D
. Тогда
CC_{1}=BK=AK=DD_{1},~CM=MD,~\angle MCC_{1}=\angle MDD_{1},
значит, треугольники MCC_{1}
и MDD_{1}
равны по двум сторонам и углу между ними, поэтому \angle CMC_{1}=\angle DMD_{1}
. Следовательно, точки C_{1}
, M
, D_{1}
лежат на одной прямой, а KM
— медиана треугольника C_{1}KD_{1}
. Тогда
KM\lt\frac{1}{2}(KC_{1}+KD_{1})=\frac{1}{2}(BC+AD).
Аналогично LN\lt\frac{1}{2}(AB+CD)
, поэтому
KM+LN\lt\frac{1}{2}(BC+AD)+\frac{1}{2}(AB+CD)=\frac{1}{2}(BC+AD+AB+CD),
что противоречит условию задачи. Следовательно, BC\parallel AD
и AB\parallel CD
, т. е. четырёхугольник ABCD
— параллелограмм.
Второй способ. Поскольку
\overrightarrow{KM}=\frac{1}{2}(\overrightarrow{BC}+\overrightarrow{AD}),~\overrightarrow{NL}=\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{DC})
(см. задачу 2097), то
\overrightarrow{KM}+\overrightarrow{NL}=\frac{1}{2}(\overrightarrow{BC}+\overrightarrow{AD}+\overrightarrow{AB}+\overrightarrow{DC}).
По условию задачи KM+NL=\frac{1}{2}(BC+AD+AB+DC)
, а это возможно только в случае, когда вектор \overrightarrow{BC}
коллинеарен вектору \overrightarrow{AD}
и вектор \overrightarrow{AB}
коллинеарен вектору \overrightarrow{DC}
. Следовательно, BC\parallel AD
и AB\parallel CD
, т. е. четырёхугольник ABCD
— параллелограмм.
Источник: Санкт-Петербургская (Ленинградская) математическая олимпиада. — 1963, 7 кл.; 1980, 9-10 классы
Источник: Журнал «Crux Mathematicorum». — 1984, № 9, задача 12 (1983, с. 304), с. 289
Источник: Петербургские математические олимпиады 1961—1993 / Под ред. Д. В. Фомина, К. П. Кохася. — СПб.—М.—Краснодар: Лань, 2007. — Задача 63.10, с. 41
Источник: Московская математическая регата. — 2006-2007, 9 класс
