3347. На сторонах треугольника ABC
как на гипотенузах строятся во внешнюю сторону равнобедренные прямоугольные треугольники ABD
, BCE
и ACF
. Докажите, что отрезки DE
и BF
равны и перпендикулярны.
Решение. Рассмотрим квадраты BCYX
и ACUV
с центрами E
и F
соответственно. При повороте вокруг точки C
на 90^{\circ}
точка A
переходит в точку U
, точка Y
— в точку B
, отрезок AY
— в отрезок UB
, значит, AY=UB
и AY\perp UB
.
Пусть M
— середина AB
. Тогда ME
и MF
— средние линии треугольников ABY
и ABY
, поэтому ME=\frac{1}{2}AY=\frac{1}{2}UB=MF
, ME\parallel AY
и MF\parallel BU
, значит, отрезки ME
и MF
равны и перпендикулярны.
При повороте вокруг точки M
на 90^{\circ}
вершина B
переходит в точку D
, точка F
— в точку E
, отрезок BF
— в отрезок DE
. Следовательно, эти отрезки равны и перпендикулярны.
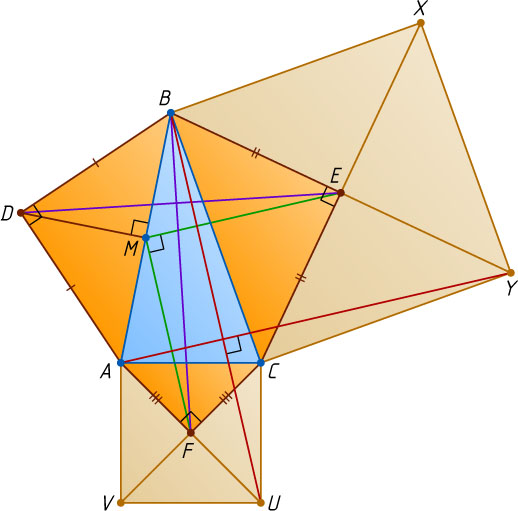
Источник: Санкт-Петербургская (Ленинградская) математическая олимпиада. — 1966, 9 кл.
Источник: Петербургские математические олимпиады 1961—1993 / Под ред. Д. В. Фомина, К. П. Кохася. — СПб.—М.—Краснодар: Лань, 2007. — Задача 66.22.
