3348. В четырёхугольнике ABCD
точки M
и N
— середины сторон AB
и CD
соответственно. Прямые AD
и BC
пересекают прямую MN
соответственно в точках P
и Q
. Докажите, что если \angle BQM=\angle APM
, то BC=AD
.
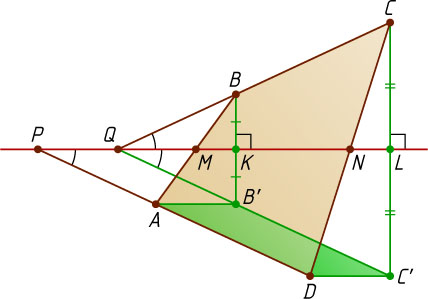
Решение. При симметрии относительно прямой MN
прямая BC
перейдёт в прямую, проходящую через точку Q
и образующую с прямой MN
угол, равный углу BQM
, а значит, APM
. Поэтому, если B'
и C'
— точки, симметричные относительно MN
вершинам B
и C
соответственно, то B'C'\parallel AD
и B'C'=BC
.
Пусть K
и L
— середины отрезков BB'
и CC'
соответственно. Тогда MK
и NL
— средние линии треугольников ABB'
и DCC'
, поэтому AB'\parallel MN\parallel DC'
.
Противоположные стороны четырёхугольника AB'C'D
попарно параллельны, значит, это параллелограмм. Следовательно, AD=B'C'=BC
. Что и требовалось доказать.
Источник: Санкт-Петербургская (Ленинградская) математическая олимпиада. — 1967, 7 кл.
Источник: Петербургские математические олимпиады 1961—1993 / Под ред. Д. В. Фомина, К. П. Кохася. — СПб.—М.—Краснодар: Лань, 2007. — Задача 67.08.
