3349. С центром в точке B
проведена окружность, касающаяся стороны AC
треугольника ABC
. Из вершин A
и C
проведены к этой окружности касательные AM
и CP
, отличные от AC
(M
и P
— точки касания). Прямая MP
пересекает прямую AB
в точке E
, а прямую BC
в точке H
. Докажите, что AH
и CE
— высоты треугольника ABC
.
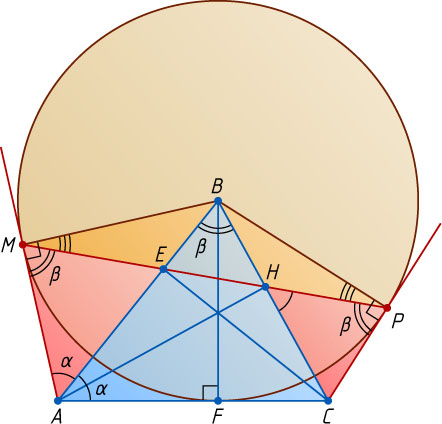
Решение. Пусть окружность касается стороны AC
в точке F
. Обозначим \angle BAC=\alpha
, \angle ABC=\beta
. Прямоугольные треугольники AMB
и AFB
равны по катету и гипотенузе, поэтому \angle ABM=\angle ABF
. Аналогично, \angle CBP=\angle CBF
, значит,
\angle MBP=2\angle ABF+2\angle CBF=2(\angle ABF+\angle CBF)=2\angle ABC=2\beta.
Из равнобедренного треугольника MBP
находим, что \angle BMP=90^{\circ}-\beta
, значит,
\angle AME=\angle AMB-\angle BMP=90^{\circ}-(90^{\circ}-\beta)=\beta,
а так как \angle MAE=\angle FAE=\alpha
, то треугольник AME
подобен треугольнику ABC
по двум углам, поэтому \frac{AE}{AC}=\frac{AM}{AB}=\cos\alpha
.
Если CE'
— высота треугольника ABC
, то \frac{AE'}{AC}=\cos\alpha
, значит, точки E
и E'
совпадают. Следовательно, CE
— высота треугольника ABC
. Аналогично, AH
— высота треугольника ABC
.
Источник: Санкт-Петербургская (Ленинградская) математическая олимпиада. — 1967, 9 кл.
Источник: Петербургские математические олимпиады 1961—1993 / Под ред. Д. В. Фомина, К. П. Кохася. — СПб.—М.—Краснодар: Лань, 2007. — Задача 67.19.
