3350. В остроугольный треугольник ABC
помещены две касающиеся окружности. Одна из них касается сторон AC
и BC
, а вторая — сторон AB
и BC
. Докажите, что сумма их радиусов больше радиуса окружности, вписанной в треугольник ABC
.
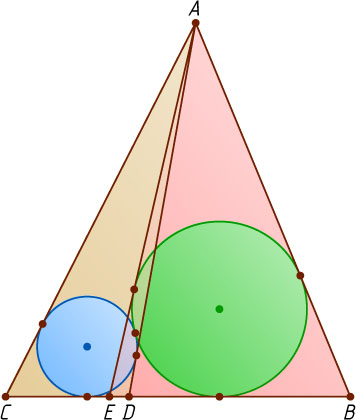
Решение. Через вершину A
проведём касательные к каждой окружности, отличные от AC
и AB
. Пусть они пересекают сторону BC
в точках D
и E
, причём окружность радиуса r_{1}
, касающаяся стороны AC
, вписана в треугольник ACD
, а окружность радиуса r_{2}
, касающаяся стороны AB
— в треугольник ABE
. Тогда треугольники ACD
и ABE
покрывают треугольник ABC
.
Пусть S_{1}
и S_{2}
— площади треугольников ACD
и ABE
соответственно, p_{1}
и p_{2}
— их полупериметры, а r
, S
и p
— радиус вписанной окружности, площадь и полупериметр треугольника ABC
. Тогда по неравенству треугольника AE\lt AC+EC
, поэтому
AE+BE\lt AC+(BE+EC),~AE+BE\lt AC+BC,
AE+BE+AB\lt AC+BC+AB,~2p_{1}\lt2p,~p_{1}\lt p.
Аналогично, p_{2}\lt p
. Следовательно,
r_{1}+r_{2}=\frac{S_{1}}{p_{1}}+\frac{S_{2}}{p_{2}}\gt\frac{S_{1}}{p}+\frac{S_{2}}{p}=\frac{S_{1}+S_{2}}{p}\gt\frac{S}{p}=r.
Что и требовалось доказать.
Источник: Московская математическая олимпиада. — 1965, XXVIII, 1-й тур, 10 класс
Источник: Гальперин Г. А., Толпыго А. К. Московские математические олимпиады. — М.: Просвещение, 1988. — № 10, с. 90
Источник: Санкт-Петербургская (Ленинградская) математическая олимпиада. — 1968, 9 кл.
Источник: Петербургские математические олимпиады 1961—1993 / Под ред. Д. В. Фомина, К. П. Кохася. — СПб.—М.—Краснодар: Лань, 2007. — Задача 68.22.
