3351. CD
— биссектриса прямого угла треугольника ABC
. DE
и DK
— биссектрисы треугольников ADC
и BDC
. Докажите, что AD^{2}+BD^{2}=(AE+BK)^{2}
.
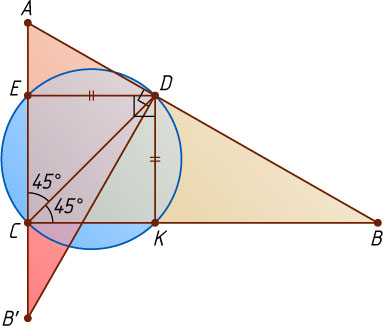
Решение. Угол EDK
— прямой как угол между биссектрисами смежных углов. Из точек C
и D
отрезок EK
виден под прямым углом, значит, эти точки лежат на окружности с диаметром EK
. Равные вписанные в эту окружность углы DCE
и DCK
опираются на равные хорды, т. е. DE=DK
.
Рассмотрим поворот на 90^{\circ}
вокруг точки D
, при котором точка K
переходит в точку E
. Поскольку AC\perp BC
, вершина B
переходит в точку B'
, лежащую на луче AC
, отрезок DB
— в равный и перпендикулярный ему отрезок DB'
, а отрезок BK
— в отрезок B'E
.
Применяя теорему Пифагора к прямоугольному треугольнику ADB'
, получим, что
AD^{2}+BD^{2}=AD^{2}+BD'^{2}=AB'^{2}=(AE+BE')^{2}=(AE+BK)^{2}.
Что и требовалось доказать.
Источник: Санкт-Петербургская (Ленинградская) математическая олимпиада. — 1971, 9 кл.
Источник: Петербургские математические олимпиады 1961—1993 / Под ред. Д. В. Фомина, К. П. Кохася. — СПб.—М.—Краснодар: Лань, 2007. — Задача 71.23.
