3352. K
и M
— точки пересечения двух окружностей. Из точки K
проведены два луча, один из которых пересекает первую окружность в точке A
, а вторую в точке B
; другой пересекает первую окружность в точке C
, вторую в точке D
. Докажите, что углы MAB
и MCD
равны.
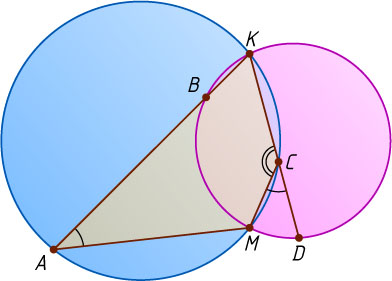
Решение. Рассмотрим случай, изображённый на рисунке. Четырёхугольник AKCM
— вписанный, поэтому
\angle BAM=\angle KAM=180^{\circ}-\angle KCM=\angle MCD.
Что и требовалось доказать. Аналогично рассматриваются остальные случаи.
Источник: Санкт-Петербургская (Ленинградская) математическая олимпиада. — 1972, 8 кл.
Источник: Петербургские математические олимпиады 1961—1993 / Под ред. Д. В. Фомина, К. П. Кохася. — СПб.—М.—Краснодар: Лань, 2007. — Задача 72.13.
