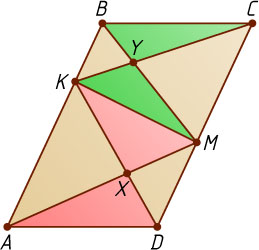
3353. На сторонах AB
и CD
параллелограмма ABCD
найдите такие точки K
и M
, чтобы площадь четырёхугольника, полученного при пересечении треугольников AMB
и CKD
, была наибольшей.
Ответ. Точки K
и M
можно взять произвольно так, чтобы отрезок KM
был параллелен AD
.
Решение. Воспользуемся следующим известным фактом. Если в трапеции (или параллелограмме) провести диагонали, то треугольники, прилежащие к боковым сторонам, равновелики.
Пусть отрезки KD
и AM
пересекаются в точке X
, а отрезки KC
и BM
— в точке Y
. Положим
k=\frac{AK}{DM}=\frac{KX}{XD}=\frac{AX}{XM}.
Тогда
S_{\triangle AXD}=S_{\triangle KXM},~S_{\triangle AKX}=kS_{\triangle KXM},~S_{\triangle DXM}=\frac{1}{k}S_{\triangle KXM}.
Поэтому
S_{AKMD}=\left(2+k+\frac{1}{k}\right)S_{\triangle KXM}\geqslant4S_{\triangle KXM},
причём равенство достигается только в случае k=1
, т. е. при KM\parallel AD
. Аналогично, S_{KBCM}\geqslant4S_{\triangle KYM}
с равенством в случае KM\parallel BC
. Складывая эти два неравенства, получаем, что S_{ABCD}\geqslant4S_{KXMY}
, или S_{KXMY}\leqslant\frac{1}{4}S_{ABCD}
. Следовательно, наибольшая возможная площадь четырёхугольника KXMY
равна \frac{1}{4}S_{ABCD}
и достигается при KM\parallel AD
.
Источник: Санкт-Петербургская (Ленинградская) математическая олимпиада. — 1973, 9 кл.
Источник: Петербургские математические олимпиады 1961—1993 / Под ред. Д. В. Фомина, К. П. Кохася. — СПб.—М.—Краснодар: Лань, 2007. — Задача 73.20.
