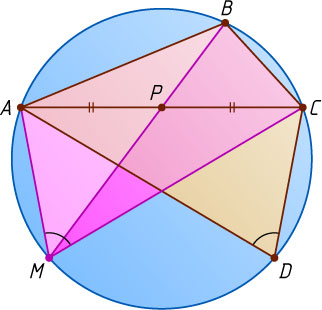
3354. Известно, что для вписанного в окружность четырёхугольника ABCD
выполнено равенство \frac{AB}{BC}=\frac{AD}{DC}
. Прямая, проходящая через вершину B
и середину диагонали AC
, пересекает окружность в точке M
, отличной от B
. Докажите, что AM=CD
.
Решение. Диагональ BM
четырёхугольника ABCM
делит пополам его диагональ AC
, значит, она делит пополам и площадь четырёхугольника ABCM
, а так как
\sin\angle BCM=\sin(180^{\circ}-\angle BAM)=\sin\angle BAM,
то AB\cdot AM=BC\cdot CM
, или \frac{AB}{BC}=\frac{CM}{AM}
. Таким образом, \frac{AD}{DC}=\frac{CM}{AM}
и \angle ADC=\angle AMC
как вписанные углы, опирающиеся на одну и ту же дугу. Поэтому треугольники ADC
и CMA
подобны, а так как AC
— их общая сторона, то эти треугольники равны. Следовательно, AM=CD
.
Источник: Санкт-Петербургская (Ленинградская) математическая олимпиада. — 1973, 9 кл.
Источник: Петербургские математические олимпиады 1961—1993 / Под ред. Д. В. Фомина, К. П. Кохася. — СПб.—М.—Краснодар: Лань, 2007. — Задача 73.19.
