3355. На окружности с центром O
лежит точка X
. На диаметре, выходящем из точки X
, возьмём точку Y
так, чтобы точка O
лежала между X
и Y
. Требуется провести через точку Y
хорду AB
так, чтобы угол AXB
был минимален.
Ответ. AB\perp XY
.
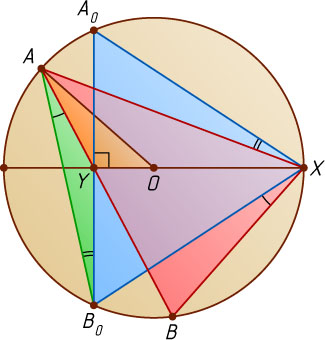
Решение. Проведём через точку Y
хорду A_{0}B_{0}
, перпендикулярную OX
, и докажем, что для любой другой хорды AB
, проходящей через точку Y
, верно неравенство \angle A_{0}XB_{0}\lt\angle AXB
.
Будем считать, что точка A
лежит на меньшей дуге A_{0}B_{0}
. Тогда
\angle AXB-\angle A_{0}XB_{0}=(\angle AXB_{0}+\angle BXB_{0})-(\angle AXA_{0}-\angle AXB_{0})=
=\angle BXB_{0}-\angle AXA_{0}=\angle BAB_{0}-\angle AB_{0}A_{0}.
Достаточно доказать, что \angle BAB_{0}\gt\angle AB_{0}A_{0}
, или YB_{0}\gt AY
(против большей стороны в треугольнике лежит больший угол).
В треугольнике OYA
угол OYA
— тупой, поэтому OA^{2}\gt OY^{2}+AY^{2}
, или
AY^{2}\lt OA^{2}-OY^{2}=OB_{0}^{2}-OY^{2}=YB_{0}^{2}.
Следовательно, YB_{0}\gt AY
. Что и требовалось доказать.
Источник: Санкт-Петербургская (Ленинградская) математическая олимпиада. — 1974, 9 кл.
Источник: Петербургские математические олимпиады 1961—1993 / Под ред. Д. В. Фомина, К. П. Кохася. — СПб.—М.—Краснодар: Лань, 2007. — Задача 74.23.
