3356. Биссектрисы AD
и CE
треугольника ABC
пересекаются в точке F
. Известно, что точки B
, D
, E
и F
лежат на одной окружности. Докажите, что радиус этой окружности не меньше радиуса вписанной в этот треугольник окружности.
Решение. Обозначим \angle ABC=\beta
. Тогда
\angle DFE=\angle AFC=90^{\circ}+\frac{1}{2}\angle ABC=90^{\circ}+\frac{\beta}{2}
(см. задачу 4770), а так как четырёхугольник BDFE
вписанный, то \angle ABC+\angle DFE=180^{\circ}
, или \beta+90^{\circ}+\frac{\beta}{2}=180^{\circ}
. Отсюда находим, что \beta=60^{\circ}
.
Биссектрисы треугольника пересекаются в одной точке, поэтому BF
— биссектриса угла DBE
, значит, \angle FBE=30^{\circ}
.
Пусть r
— радиус вписанной окружности треугольника ABC
, а r_{1}
— радиус окружности, описанной около четырёхугольника DBEF
. Тогда
r_{1}=\frac{EF}{2\sin30^{\circ}}=EF\geqslant r,
так как F
— центр вписанной окружности треугольника ABC
(точка пересечения его биссектрис), а r
— длина перпендикуляра, опущенного из точки F
на сторону AB
. Что и требовалось доказать.
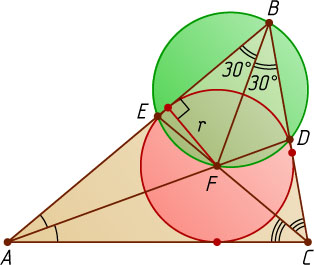
Источник: Санкт-Петербургская (Ленинградская) математическая олимпиада. — 1975, 8 кл.
Источник: Петербургские математические олимпиады 1961—1993 / Под ред. Д. В. Фомина, К. П. Кохася. — СПб.—М.—Краснодар: Лань, 2007. — Задача 75.15.
